Unitary transformation
unitary mapping
A linear transformation  of a unitary space
of a unitary space  preserving the inner product of vectors, i.e. such that for any vectors
preserving the inner product of vectors, i.e. such that for any vectors  and
and  of
of  one has the equality
one has the equality
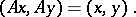 |
A unitary transformation preserves, in particular, the length of a vector. Conversely, if a linear transformation of a unitary space preserves the lengths of all vectors, then it is unitary. The eigenvalues of a unitary transformation have modulus 1; the eigenspaces corresponding to different eigenvalues are orthogonal.
A linear transformation  of a finite-dimensional unitary space
of a finite-dimensional unitary space  is unitary if and only if it satisfies any of the following conditions:
is unitary if and only if it satisfies any of the following conditions:
1) in any orthonormal basis the transformation  corresponds to a unitary matrix;
corresponds to a unitary matrix;
2)  maps any orthonormal basis to an orthonormal basis;
maps any orthonormal basis to an orthonormal basis;
3) in  there exists an orthonormal basis of eigenvectors of
there exists an orthonormal basis of eigenvectors of 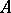 , and, moreover,
, and, moreover, 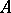 has in this basis a diagonal matrix with diagonal entries of modulus 1.
has in this basis a diagonal matrix with diagonal entries of modulus 1.
The unitary transformations of a given unitary space form a group under multiplication of transformations (called the unitary group).
Comments
References
| [a1] | W.H. Greub, "Linear algebra" , Springer (1975) pp. 338ff |
Unitary transformation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Unitary_transformation&oldid=17263