Unitary representation
of a topological group
A representation of the topological group by unitary operators in a Hilbert space (cf. Unitary operator). The theory of unitary representations is one of the most developed parts of the theory of representations of topological groups, which is connected both with its numerous applications and with the presence of a number of properties facilitating the study of unitary representations. Thus, any unitary representation is completely reducible; for a unitary representation the conditions of complete irreducibility, tensor irreducibility, topological irreducibility, and operator irreducibility are all equivalent; from the continuity of a unitary representation with respect to the weak operator topology follows its continuity with respect to the strong operator topology; for a unitary representation one can define the operation of tensor product of representations, as well as the operation of passing to the contragredient representation (in the Hilbert space which is the complex conjugate of the given one), and for the operations of direct sum, tensor product and passing to the contragredient representation there hold a number of natural algebraic relations.
The most highly developed part of the general theory of unitary representations and the most important in applications is the theory of unitary representations of locally compact groups. There does not exist a description of the class of groups for which the unitary representations (or the irreducible unitary representations) separate the points of the group (1992). However, if the group 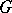 is locally compact, then for every non-identity element
is locally compact, then for every non-identity element  there exists an irreducible unitary representation
there exists an irreducible unitary representation  of
of 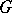 such that
such that 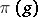 is a non-identity operator in the space of the representation (the Gel'fand–Raikov theorem). Further, between the non-degenerate symmetric representations of the group algebra
is a non-identity operator in the space of the representation (the Gel'fand–Raikov theorem). Further, between the non-degenerate symmetric representations of the group algebra 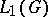 (constructed with the left Haar measure) and the continuous unitary representations of the group
(constructed with the left Haar measure) and the continuous unitary representations of the group 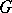 there exists a natural one-one correspondence
there exists a natural one-one correspondence 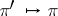 , defined by the formula
, defined by the formula
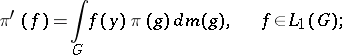 |
moreover, the representation 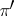 of the algebra
of the algebra 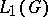 is topologically irreducible (is a quotient representation, a representation of a given type, a representation equivalent or quasi-equivalent to another) if and only if the corresponding unitary representation
is topologically irreducible (is a quotient representation, a representation of a given type, a representation equivalent or quasi-equivalent to another) if and only if the corresponding unitary representation 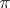 of the group has the same property.
of the group has the same property.
The theory of cyclic unitary representations of a locally compact group 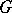 , which is related to the theory of positive linear functionals on
, which is related to the theory of positive linear functionals on 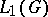 , may be studied by means of appropriate spherical functions (cf. Representation of a topological group). The spherical functions connected with unitary representations of a locally compact group
, may be studied by means of appropriate spherical functions (cf. Representation of a topological group). The spherical functions connected with unitary representations of a locally compact group 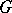 are continuous positive-definite functions on the group, and, conversely, any continuous positive-definite function on
are continuous positive-definite functions on the group, and, conversely, any continuous positive-definite function on 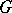 , equal to 1 at the identity, is a spherical function connected with a cyclic unitary representation (and defined by the cyclic vector of this unitary representation). The set
, equal to 1 at the identity, is a spherical function connected with a cyclic unitary representation (and defined by the cyclic vector of this unitary representation). The set 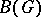 of all linear combinations of continuous positive-definite functions on
of all linear combinations of continuous positive-definite functions on 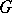 forms a commutative Banach algebra (relative to the usual multiplication), called the Fourier–Stieltjes algebra of
forms a commutative Banach algebra (relative to the usual multiplication), called the Fourier–Stieltjes algebra of 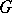 ; the closed ideal
; the closed ideal 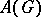 in
in 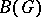 generated by the functions of the form
generated by the functions of the form 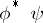 , where
, where 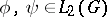 , is called the Fourier algebra of
, is called the Fourier algebra of 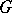 . The Banach algebras
. The Banach algebras 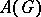 and
and 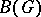 define the group
define the group 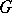 up to an isomorphism or anti-isomorphism.
up to an isomorphism or anti-isomorphism.
On the set 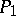 of continuous positive-definite functions on
of continuous positive-definite functions on 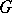 , equal to 1 at the unit element of the group, the topology of uniform convergence on compact subsets of
, equal to 1 at the unit element of the group, the topology of uniform convergence on compact subsets of 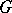 coincides with the weak topology defined by the duality between
coincides with the weak topology defined by the duality between 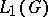 and
and 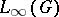 and the imbedding of
and the imbedding of 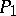 in
in 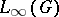 . Any function
. Any function 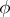 in
in 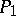 is the limit (in this topology) of a net of convex combinations of positive-definite functions, connected with irreducible unitary representations of
is the limit (in this topology) of a net of convex combinations of positive-definite functions, connected with irreducible unitary representations of 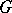 ; if further
; if further 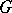 is a separable group, then there exists a positive measure
is a separable group, then there exists a positive measure 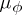 on the compact set of continuous positive-definite functions on
on the compact set of continuous positive-definite functions on 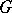 , not exceeding 1 in absolute value, concentrated on
, not exceeding 1 in absolute value, concentrated on 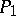 and such that
and such that
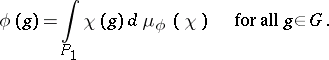 |
The construction of unitary representations from positive-definite functions allows a generalization to the case of positive-definite measures on 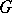 . If
. If 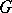 is a separable group, then any representation defined by a positive-definite measure is cyclic.
is a separable group, then any representation defined by a positive-definite measure is cyclic.
A unitary representation 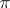 of a locally compact group
of a locally compact group 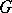 in a Hilbert space
in a Hilbert space 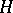 admits a decomposition as a topological direct integral of irreducible unitary representations of
admits a decomposition as a topological direct integral of irreducible unitary representations of  , if either
, if either 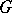 or
or 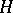 is separable (for non-separable groups and spaces this is not generally true). Moreover, in this case the unitary representation
is separable (for non-separable groups and spaces this is not generally true). Moreover, in this case the unitary representation 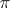 admits an essentially unique decomposition as a direct integral of quotient representations. In connection with this fact an essential role is played by the dual space
admits an essentially unique decomposition as a direct integral of quotient representations. In connection with this fact an essential role is played by the dual space 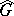 (the quotient space of the space of irreducible unitary representations of
(the quotient space of the space of irreducible unitary representations of 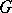 , considered with the topology defined by uniform convergence of matrix entries on compact sets and with the Borel structure subordinate to this topology, with respect to the equivalence defined by unitary equivalence of unitary representations) and the quasi-dual space
, considered with the topology defined by uniform convergence of matrix entries on compact sets and with the Borel structure subordinate to this topology, with respect to the equivalence defined by unitary equivalence of unitary representations) and the quasi-dual space 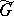 (the quotient space of the space of quotient representations of
(the quotient space of the space of quotient representations of 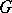 , considered with the Borel structure subordinate to the topology of uniform convergence of matrix entries on compact sets). Thus,
, considered with the Borel structure subordinate to the topology of uniform convergence of matrix entries on compact sets). Thus, 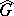 is a topological and a Borel space, and
is a topological and a Borel space, and 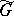 is a Borel space, which for a separable group may be equipped with the topology extending the topology on
is a Borel space, which for a separable group may be equipped with the topology extending the topology on  . The group
. The group  is said to be a group of type I if all its quotient representations are of type I; for such groups questions of the theory of unitary representations can be solved more simply than in the general case. Groups of type I include algebraic Lie groups and algebraic Chevalley groups over
is said to be a group of type I if all its quotient representations are of type I; for such groups questions of the theory of unitary representations can be solved more simply than in the general case. Groups of type I include algebraic Lie groups and algebraic Chevalley groups over  -adic fields, nilpotent Lie groups, and others. A characterization of the simply-connected solvable Lie groups of type I is known. A group
-adic fields, nilpotent Lie groups, and others. A characterization of the simply-connected solvable Lie groups of type I is known. A group 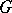 is called a CCR-group if for any irreducible unitary representation
is called a CCR-group if for any irreducible unitary representation 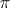 of
of 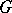 the image
the image 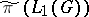 under the representation
under the representation  is contained in the set
is contained in the set 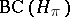 of compact operators in the space
of compact operators in the space 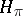 of the representation
of the representation  . Every CCR-group is of type I. A group of type I is a CCR-group if and only if its dual space is a
. Every CCR-group is of type I. A group of type I is a CCR-group if and only if its dual space is a 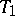 -space. Nilpotent Lie groups and linear semi-simple Lie groups are CCR-groups. The image of the representation
-space. Nilpotent Lie groups and linear semi-simple Lie groups are CCR-groups. The image of the representation 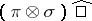 is contained in
is contained in  for all irreducible unitary representations
for all irreducible unitary representations 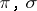 of
of 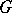 if and only if all irreducible unitary representations are finite-dimensional.
if and only if all irreducible unitary representations are finite-dimensional.
A separable locally compact group is of type I if and only if its dual space satisfies the separation axiom 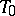 . Other topological properties of the spectra (
. Other topological properties of the spectra (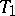 -separation, the Hausdorff property, discreteness, and others) are also connected with properties of the group. A particularly close link between the topological and algebraic properties of the group and its dual space exists in classes of groups satisfying various compactness conditions. Among these classes of locally compact groups are included: 1) the class
-separation, the Hausdorff property, discreteness, and others) are also connected with properties of the group. A particularly close link between the topological and algebraic properties of the group and its dual space exists in classes of groups satisfying various compactness conditions. Among these classes of locally compact groups are included: 1) the class 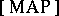 of maximal almost-periodic groups (admitting a continuous imbedding in a compact group); 2) the class
of maximal almost-periodic groups (admitting a continuous imbedding in a compact group); 2) the class 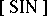 of groups containing a fundamental system of neighbourhoods of the unit element that are invariant under inner automorphisms; 3) the class
of groups containing a fundamental system of neighbourhoods of the unit element that are invariant under inner automorphisms; 3) the class 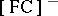 of groups with pre-compact classes of conjugate elements; 4) the class
of groups with pre-compact classes of conjugate elements; 4) the class 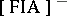 of groups with a pre-compact group of inner automorphisms; 5) the class
of groups with a pre-compact group of inner automorphisms; 5) the class 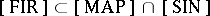 of groups all irreducible unitary representations of which are finite-dimensional; and 6) the class
of groups all irreducible unitary representations of which are finite-dimensional; and 6) the class 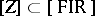 of groups whose quotient group by the centre is compact. The dual spaces of groups of class
of groups whose quotient group by the centre is compact. The dual spaces of groups of class  are Hausdorff spaces, and a group of class
are Hausdorff spaces, and a group of class 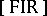 is discrete if and only if its dual space is compact (though not necessarily separable). The theory of unitary representations of groups of class
is discrete if and only if its dual space is compact (though not necessarily separable). The theory of unitary representations of groups of class  is connected with the theory of almost-periodic functions on locally compact groups.
is connected with the theory of almost-periodic functions on locally compact groups.
The character of a unitary representation of a locally compact group 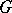 is the faithful normal semi-finite trace
is the faithful normal semi-finite trace 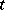 (cf. Trace on a
(cf. Trace on a 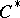 -algebra) on the set of positive elements of the von Neumann algebra
-algebra) on the set of positive elements of the von Neumann algebra 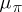 generated by the family
generated by the family 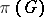 , such that the set of elements
, such that the set of elements  of the group
of the group 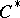 -algebra
-algebra 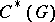 of
of 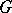 (the enveloping
(the enveloping 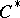 -algebra of the group algebra
-algebra of the group algebra 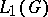 ) for which
) for which 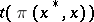 is finite, goes over into the set generated by the von Neumann algebra
is finite, goes over into the set generated by the von Neumann algebra 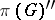 . If
. If 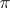 is a quotient representation (respectively, an irreducible unitary representation), then the character
is a quotient representation (respectively, an irreducible unitary representation), then the character 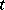 defines the unitary representation
defines the unitary representation  uniquely up to a quasi-equivalence (respectively, an equivalence). If
uniquely up to a quasi-equivalence (respectively, an equivalence). If 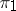 ,
,  are irreducible unitary representations of
are irreducible unitary representations of 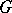 with characters
with characters 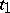 ,
,  , respectively, then the product of these traces defines a trace on the von Neumann algebra induced by the unitary representation
, respectively, then the product of these traces defines a trace on the von Neumann algebra induced by the unitary representation 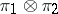 . If this trace is the character of the representation
. If this trace is the character of the representation 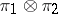 , then (for separable groups or separable representation spaces) it defines a decomposition of the unitary representation
, then (for separable groups or separable representation spaces) it defines a decomposition of the unitary representation 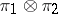 into a direct integral of quotient representations with a trace with respect to a uniquely defined measure (the Plancherel measure for
into a direct integral of quotient representations with a trace with respect to a uniquely defined measure (the Plancherel measure for 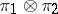 ) on the quasi-spectrum
) on the quasi-spectrum 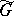 . The determination of the Plancherel measure on the tensor product of unitary representations is one of the general problems in the theory of unitary representations; in a number of cases (in particular, for the groups
. The determination of the Plancherel measure on the tensor product of unitary representations is one of the general problems in the theory of unitary representations; in a number of cases (in particular, for the groups 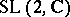 ,
,  , certain unitary representations of other semi-simple Lie groups, and certain solvable Lie groups) this problem has been solved (using the spectral decomposition of the Laplace operator, the orbit method or the horosphere method).
, certain unitary representations of other semi-simple Lie groups, and certain solvable Lie groups) this problem has been solved (using the spectral decomposition of the Laplace operator, the orbit method or the horosphere method).
Sometimes one understands by the character of a unitary representation 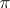 in a Hilbert space
in a Hilbert space 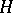 a linear functional
a linear functional 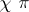 on a translation-invariant subalgebra
on a translation-invariant subalgebra 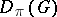 of
of 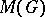 , defined by the equation
, defined by the equation  ,
,  , where
, where  is the representation of
is the representation of 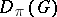 defined by
defined by 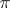 (assuming that
(assuming that 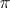 is uniquely determined by the representation
is uniquely determined by the representation 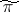 , the operators of
, the operators of 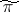 are nuclear and the mapping
are nuclear and the mapping 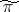 of the algebra
of the algebra 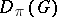 into the space of nuclear operators is continuous). The characters of irreducible unitary representations of semi-simple and nilpotent Lie groups are defined by generalized functions, which in the case of semi-simple groups are measurable and locally integrable. The characters of irreducible unitary representations of solvable Lie groups of type I are defined, generally speaking, only on a subalgebra of the algebra
into the space of nuclear operators is continuous). The characters of irreducible unitary representations of semi-simple and nilpotent Lie groups are defined by generalized functions, which in the case of semi-simple groups are measurable and locally integrable. The characters of irreducible unitary representations of solvable Lie groups of type I are defined, generally speaking, only on a subalgebra of the algebra  of infinitely-differentiable functions on
of infinitely-differentiable functions on 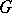 with compact support. In general, the calculation of the characters is based on formulas for the characters of induced representations.
with compact support. In general, the calculation of the characters is based on formulas for the characters of induced representations.
A compact subgroup  of a group
of a group 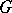 is called rich (or massive) if the restriction of any unitary representation
is called rich (or massive) if the restriction of any unitary representation  of
of 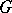 to
to 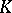 contains any irreducible unitary representation
contains any irreducible unitary representation 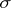 of
of 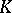 with finite multiplicity. Let
with finite multiplicity. Let 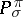 be the projector from the space
be the projector from the space 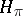 of the representation
of the representation 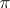 onto the subspace on which that representation of
onto the subspace on which that representation of 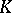 acts which is a multiple of
acts which is a multiple of  ; the functions of the form
; the functions of the form
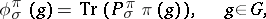 |
are called 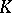 -spherical functions of the representation
-spherical functions of the representation 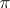 (cf. Representation function). A group
(cf. Representation function). A group 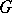 with a rich compact subgroup is of type I; every irreducible unitary representation of
with a rich compact subgroup is of type I; every irreducible unitary representation of  has a character and is defined uniquely up to an equivalence by any non-zero spherical function; the dual space
has a character and is defined uniquely up to an equivalence by any non-zero spherical function; the dual space  of the group
of the group 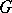 can be expressed as a countable union of (intersecting) locally compact Hausdorff spaces (describing the
can be expressed as a countable union of (intersecting) locally compact Hausdorff spaces (describing the 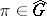 for which
for which  for a given
for a given 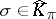 , and the dimension of the corresponding projector
, and the dimension of the corresponding projector 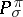 has a given value). The linear semi-simple Lie groups and the
has a given value). The linear semi-simple Lie groups and the 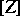 -groups are groups with rich compact subgroups.
-groups are groups with rich compact subgroups.
Let 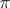 be a unitary representation of a group
be a unitary representation of a group 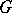 in a Hilbert space
in a Hilbert space 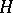 , and let
, and let 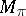 be the von Neumann algebra generated by the family
be the von Neumann algebra generated by the family 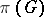 . The representation
. The representation  is said to be trace-admissible if there exists a trace on
is said to be trace-admissible if there exists a trace on  which is a character for
which is a character for 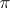 . By a trace on the group
. By a trace on the group 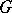 one understands a semi-finite lower semi-continuous trace on
one understands a semi-finite lower semi-continuous trace on 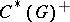 ; a trace on
; a trace on 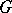 is called a character of
is called a character of  if the corresponding unitary representation of
if the corresponding unitary representation of 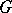 is a quotient representation. There is a canonical one-to-one correspondence between the set of characters of
is a quotient representation. There is a canonical one-to-one correspondence between the set of characters of 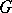 , defined up to a positive factor, and the set of quasi-equivalence classes of trace-admissible quotient representations of
, defined up to a positive factor, and the set of quasi-equivalence classes of trace-admissible quotient representations of 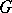 ; moreover, a quotient representation of finite type corresponds to a continuous central positive-definite function on
; moreover, a quotient representation of finite type corresponds to a continuous central positive-definite function on 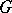 .
.
The regular representation of a locally compact group 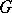 in the Hilbert space
in the Hilbert space 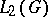 is a faithful continuous unitary representation; the
is a faithful continuous unitary representation; the 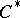 -algebra generated by the image of the corresponding representation of the algebra
-algebra generated by the image of the corresponding representation of the algebra 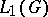 is called the reduced
is called the reduced 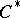 -algebra of the group
-algebra of the group 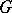 and is denoted by
and is denoted by 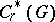 ; let
; let  be the kernel of the canonical epimorphism of
be the kernel of the canonical epimorphism of 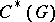 onto
onto 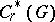 defined by the regular representation. The group
defined by the regular representation. The group 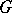 is amenable, i.e. there is an invariant mean on
is amenable, i.e. there is an invariant mean on 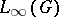 , if and only if
, if and only if 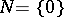 (bounded representations of amenable groups in a Hilbert space are equivalent to unitary representations). The family of unitary representations
(bounded representations of amenable groups in a Hilbert space are equivalent to unitary representations). The family of unitary representations 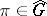 for which the kernel of the corresponding representation of
for which the kernel of the corresponding representation of 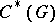 contains
contains 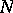 is called the fundamental series. The remaining unitary representations
is called the fundamental series. The remaining unitary representations 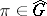 form the supplementary series.
form the supplementary series.
Let 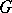 be a unimodular separable locally compact group of type I, and let
be a unimodular separable locally compact group of type I, and let 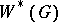 be the von Neumann algebra
be the von Neumann algebra 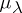 , where
, where 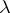 is the regular unitary representation of
is the regular unitary representation of 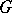 . There exists a unique positive measure
. There exists a unique positive measure 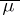 on the spectrum
on the spectrum  of
of 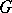 satisfying the condition
satisfying the condition
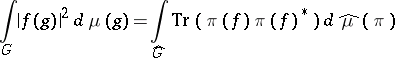 | (*) |
for all 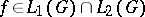 . The measure
. The measure 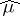 is called the Plancherel measure. Further, there exists an isomorphism of the space
is called the Plancherel measure. Further, there exists an isomorphism of the space 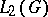 onto a direct integral of Hilbert–Schmidt operators in the space of the representation
onto a direct integral of Hilbert–Schmidt operators in the space of the representation 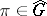 with respect to the measure
with respect to the measure 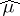 , which transforms the left-regular unitary representation
, which transforms the left-regular unitary representation 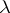 into a direct integral of unitary representations that are multiples of
into a direct integral of unitary representations that are multiples of 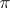 , and transforms the trace on
, and transforms the trace on 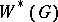 defined by the trace
defined by the trace 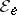 on
on 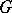 (
(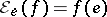 for
for 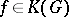 ) into the direct integral of traces,
) into the direct integral of traces, 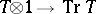 on
on 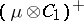 . The trace
. The trace 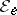 on
on 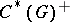 coincides with the trace
coincides with the trace 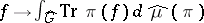 ,
, 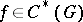 . The formula (*) is called the Plancherel formula; it admits a generalization to non-separable unimodular locally compact groups of type I, as well as to non-unimodular separable locally compact groups and separable groups not of type I. One of the tasks of the theory of unitary representations is the explicit construction of a Plancherel measure for a given locally compact group. This problem has only been partly solved (for example, for semi-simple real Lie groups, for solvable Lie groups of type I, as well as for certain groups of motions, certain Chevalley groups, and certain groups satisfying a compactness condition). The decomposition of the regular unitary representation and the Plancherel formula are connected with the theory of square-integrable representations, discrete series (of representations) and integrable representations (cf. Integrable representation).
. The formula (*) is called the Plancherel formula; it admits a generalization to non-separable unimodular locally compact groups of type I, as well as to non-unimodular separable locally compact groups and separable groups not of type I. One of the tasks of the theory of unitary representations is the explicit construction of a Plancherel measure for a given locally compact group. This problem has only been partly solved (for example, for semi-simple real Lie groups, for solvable Lie groups of type I, as well as for certain groups of motions, certain Chevalley groups, and certain groups satisfying a compactness condition). The decomposition of the regular unitary representation and the Plancherel formula are connected with the theory of square-integrable representations, discrete series (of representations) and integrable representations (cf. Integrable representation).
A complete description of the irreducible unitary representations of locally compact groups is unknown, even in the case of Lie groups. It has been obtained only for solvable Lie groups of type I, certain reductive Lie groups, as well as for Chevalley groups (of low dimensions), certain nilpotent locally compact Lie groups and certain semi-direct products. In this description a decisive role is played by the inducing operator (and its generalizations); in particular, the orbit method (and its generalizations). The problem of studying more general projective unitary representations and unitary representations with multipliers is connected with the theory of ordinary unitary representations by means of the theory of (continuous or Borel) cohomology groups. For groups that are not of type I a complete description of the quotient representations (up to a quasi-equivalence) does not exist, although for some of them a description of the quotient representations of finite type has been obtained.
The theory of unitary representations plays a fundamental role in the theory of series on (Banach and topological) group algebras: in the study of Wiener properties and complete symmetry, in the description of the maximal one-sided and two-sided ideals, etc. The theory of unitary representations plays an important role, also, in questions of representation theory and harmonic analysis, requiring a use of non-unitary representations — as in the construction of the bounded series and the supplementary series; in the definition of operators in explicit form; in splitting representations from the analytic continuation of the basic series of unitary representations; in the study of intertwining of completely-reducible representations; in the development of harmonic analysis in function spaces on groups and homogeneous spaces other than the space 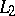 ; and in the study on the structure and properties of group algebras (measure algebras, the algebra
; and in the study on the structure and properties of group algebras (measure algebras, the algebra 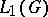 , the topological algebra
, the topological algebra  ).
).
References
| [1] | A.A. Kirillov, "Elements of the theory of representations" , Springer (1976) (Translated from Russian) |
| [2] | A.I. Shtern, "Theory of group representations" , Springer (1982) (Translated from Russian) |
| [3] | M.A. Naimark, "Normed rings" , Reidel (1984) (Translated from Russian) |
| [4] | D.P. Zhelobenko, "Compact Lie groups and their representations" , Amer. Math. Soc. (1973) (Translated from Russian) |
| [5] | D.P. Zhelobenko, A.I. Shtern, "Representations of Lie groups" , Moscow (1983) (In Russian) |
| [6] | J. Dixmier, "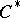 algebras" , North-Holland (1977) (Translated from French) algebras" , North-Holland (1977) (Translated from French) |
| [7] | I.M. Gel'fand, M.I. Graev, I.I. Pyatetskii-Shapiro, "Generalized functions" , 6. Representation theory and automorphic functions , Saunders (1969) (Translated from Russian) |
| [8] | N.Ya. Vilenkin, "Special functions and the theory of group representations" , Amer. Math. Soc. (1968) (Translated from Russian) |
| [9] | A.O. Barut, R. Raçzka, "Theory of group representations and applications" , 1–2 , PWN (1977) |
| [10] | A.U. Klimyk, "Matrix elements and Clebsch–Gordan coefficients of group representations" , Kiev (1979) (In Russian) |
| [11] | G.W. Mackey, "Unitary group representations in physics, probability and number theory" , Benjamin/Cummings (1978) |
| [12] | P. Bernal, et al., "Répresentation des groupes de Lie résolubles" , Dunod (1972) |
| [13] | J. Brezin, "Harmonic analysis on compact solvmanifolds" , Springer (1977) |
| [14] | G. Carmona (ed.) M. Vergne (ed.) , Non-commutative harmonic analysis (Marseille, 1978) , Lect. notes in math. , 728 , Springer (1979) |
Comments
See also (the editorial comments to) Representation function and Spherical functions for another usage of the term "spherical function" . In [8] and [a1] a subgroup 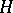 of
of 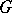 is called massive if the trivial representation of
is called massive if the trivial representation of 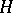 occurs with multiplicity at most
occurs with multiplicity at most 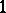 in each irreducible representation of
in each irreducible representation of 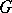 . See [8], [10] and [a1] for interpretations of special functions as matrix elements of unitary representations.
. See [8], [10] and [a1] for interpretations of special functions as matrix elements of unitary representations.
References
| [a1] | N.Ya. Vilenkin, A.U. Klimyk, "Representation of Lie groups and special functions" , 1 , Kluwer (1991) (Translated from Russian) |
Unitary representation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Unitary_representation&oldid=14274