Unitary matrix
From Encyclopedia of Mathematics
A square matrix  over the field
over the field  of complex numbers, whose rows form an orthonormal system, i.e.
of complex numbers, whose rows form an orthonormal system, i.e.
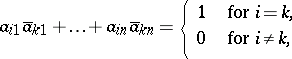 |
 . In a unitary space, transformation from one orthonormal basis to another is accomplished by a unitary matrix. The matrix of a unitary transformation relative to an orthonormal basis is also (called) a unitary matrix. A square matrix
. In a unitary space, transformation from one orthonormal basis to another is accomplished by a unitary matrix. The matrix of a unitary transformation relative to an orthonormal basis is also (called) a unitary matrix. A square matrix  with complex entries is unitary if and only if it satisfies any of the following conditions:
with complex entries is unitary if and only if it satisfies any of the following conditions:
1)  ;
;
2)  ;
;
3)  ;
;
4) the columns of  form an orthonormal system (here
form an orthonormal system (here  is the conjugate transposed of
is the conjugate transposed of 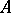 ).
).
The determinant of a unitary matrix is a complex number of modulus one.
Comments
References
| [a1] | W. Noll, "Finite dimensional spaces" , M. Nijhoff (1987) pp. 63 |
| [a2] | W.H. Greub, "Linear algebra" , Springer (1975) pp. 329 |
How to Cite This Entry:
Unitary matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Unitary_matrix&oldid=13327
Unitary matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Unitary_matrix&oldid=13327
This article was adapted from an original article by O.A. Ivanova (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article