Uniqueness set
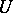 -set
-set
A set 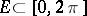 such that a trigonometric series that converges to zero at each point of
such that a trigonometric series that converges to zero at each point of 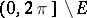 is the zero series. A set that is not a
is the zero series. A set that is not a 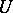 -set is a called a set of non-uniqueness, or an
-set is a called a set of non-uniqueness, or an 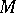 -set. These concepts are related to the problem of the uniqueness of the representation of a function by a trigonometric series converging to it everywhere, except perhaps on a given set
-set. These concepts are related to the problem of the uniqueness of the representation of a function by a trigonometric series converging to it everywhere, except perhaps on a given set 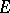 . G. Cantor (1872) showed that a finite set (including the empty set) is a set of uniqueness, and the extension of this result to infinite sets led him to the creation of set theory.
. G. Cantor (1872) showed that a finite set (including the empty set) is a set of uniqueness, and the extension of this result to infinite sets led him to the creation of set theory.
Sets of positive Lebesgue measure are always 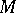 -sets. Any countable set is a
-sets. Any countable set is a 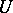 -set. There exists perfect sets (cf. Perfect set) of measure zero that are
-set. There exists perfect sets (cf. Perfect set) of measure zero that are 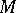 -sets (D.E. Men'shov, 1916), and ones that are
-sets (D.E. Men'shov, 1916), and ones that are 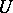 -sets (N.K. Bari, 1921); for example, the Cantor set with a constant rational ratio
-sets (N.K. Bari, 1921); for example, the Cantor set with a constant rational ratio 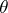 is a
is a 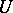 -set if and only
-set if and only  is an integer, that is, whether a set of numbers is a
is an integer, that is, whether a set of numbers is a 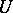 -set or an
-set or an 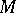 -set depends on the arithmetical nature of the numbers forming it. However, there exist sets
-set depends on the arithmetical nature of the numbers forming it. However, there exist sets 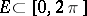 of full measure (so-called
of full measure (so-called 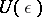 -sets) such that any trigonometric series that converges to zero at every point of
-sets) such that any trigonometric series that converges to zero at every point of 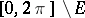 and has coefficients that are
and has coefficients that are 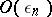 , where
, where 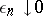 , is the zero series.
, is the zero series.
The concepts of 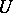 -sets and
-sets and 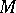 -sets can be generalized to Fourier–Stieltjes series.
-sets can be generalized to Fourier–Stieltjes series.
References
| [1] | N.K. [N.K. Bari] Bary, "A treatise on trigonometric series" , Pergamon (1964) (Translated from Russian) |
| [2] | A. Zygmund, "Trigonometric series" , 1–2 , Cambridge Univ. Press (1988) |
| [3] | N.K. Bari, "The uniqueness problem of the representation of functions by trigonometric series" Transl. Amer. Math. Soc. (1) , 3 (1951) pp. 107–195 Uspekhi Mat. Nauk , 4 : 3 (1949) pp. 3–68 |
Comments
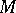 -sets are also called sets of multiplicity. A set
-sets are also called sets of multiplicity. A set 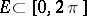 such that a Fourier–Stieltjes series that converges to zero at each point of
such that a Fourier–Stieltjes series that converges to zero at each point of 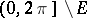 is the zero series, is called a
is the zero series, is called a  -set, or a set of extended uniqueness. A set that is not a
-set, or a set of extended uniqueness. A set that is not a 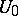 -set is called an
-set is called an 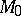 -set, or a set of restricted multiplicity. A set
-set, or a set of restricted multiplicity. A set 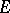 is a
is a 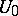 -set if and only if it does not support a non-zero Rajchman measure, that is, a measure whose Fourier–Stieltjes coefficients tend to zero at infinity. In the modern theory,
-set if and only if it does not support a non-zero Rajchman measure, that is, a measure whose Fourier–Stieltjes coefficients tend to zero at infinity. In the modern theory, 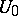 -sets play a more prominent role than
-sets play a more prominent role than 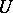 -sets. In 1983, R. Lyons proved that the Rajchman measures are exactly the measures that annihilate all
-sets. In 1983, R. Lyons proved that the Rajchman measures are exactly the measures that annihilate all 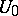 -sets. In [a1]–[a3] many more results are given, e.g. relating uniqueness sets with Helson sets and sets of spectral synthesis (cf. Harmonic analysis, abstract).
-sets. In [a1]–[a3] many more results are given, e.g. relating uniqueness sets with Helson sets and sets of spectral synthesis (cf. Harmonic analysis, abstract).
Consider a closed interval 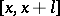 of length
of length 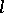 . Let
. Let 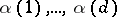 ,
, 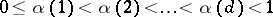 , be
, be 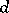 numbers and consider the
numbers and consider the 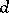 closed intervals
closed intervals 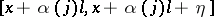 , where
, where 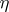 is small enough so that the intervals have no points in common. Retain only these intervals (and throw the complementary intervals away). This is referred to as performing a dissection of type
is small enough so that the intervals have no points in common. Retain only these intervals (and throw the complementary intervals away). This is referred to as performing a dissection of type
 |
Now start with any interval of length 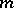 . Perform a dissection of type
. Perform a dissection of type 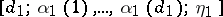 , perform a dissection of type
, perform a dissection of type 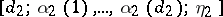 on each of the intervals obtained, etc. After
on each of the intervals obtained, etc. After 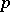 iterations one has
iterations one has 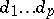 intervals, each of length
intervals, each of length 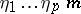 , and as
, and as 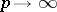 the final result is a closed set
the final result is a closed set 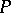 of measure
of measure  (the limit exists). If
(the limit exists). If 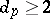 for all
for all 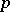 , the resulting
, the resulting 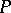 is perfect (cf. Perfect set) and non-dense. For
is perfect (cf. Perfect set) and non-dense. For 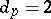 and
and 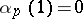 ,
, 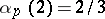 ,
, 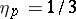 for all
for all 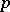 , one obtains the Cantor set. Taking successive dissections of type
, one obtains the Cantor set. Taking successive dissections of type 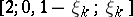 yields a so-called set of Cantor type. If
yields a so-called set of Cantor type. If 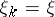 for all
for all 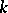 , one speaks of a set of Cantor type of constant ratio (of dissection). Cf. [2], pp. 194ff, for more details.
, one speaks of a set of Cantor type of constant ratio (of dissection). Cf. [2], pp. 194ff, for more details.
References
| [a1] | C.C. Graham, O.C. McGehee, "Essays in commutative harmonic analysis" , Springer (1979) pp. Chapt. 5 |
| [a2] | J.-P. Kahane, "Séries de Fourier absolument convergentes" , Springer (1970) |
| [a3] | A.S. Kechris, A. Louveau, "Descriptive set theory and the structure of sets of uniqueness" , Cambridge Univ. Press (1987) |
Uniqueness set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Uniqueness_set&oldid=16760