Uniform algebra
A subalgebra  , closed with respect to the topology of uniform convergence, of the algebra
, closed with respect to the topology of uniform convergence, of the algebra  of continuous functions on a compactum
of continuous functions on a compactum  that contains all constant functions and separates the points of
that contains all constant functions and separates the points of  . The last condition means that for each pair
. The last condition means that for each pair  of distinct points in
of distinct points in  there is a function
there is a function  in
in  for which
for which  . Uniform algebras are usually provided with the sup norm:
. Uniform algebras are usually provided with the sup norm:
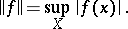 |
Here  . Every Banach algebra with an identity (even without assuming commutativity) and with a norm satisfying the latter condition is isomorphic to a uniform algebra.
. Every Banach algebra with an identity (even without assuming commutativity) and with a norm satisfying the latter condition is isomorphic to a uniform algebra.
The uniform algebras form an important subclass of the class of commutative Banach algebras (cf. Commutative Banach algebra) over the field of complex numbers 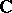 .
.
To each point 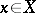 corresponds a homomorphism
corresponds a homomorphism 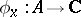 , defined by
, defined by 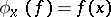 . Therefore
. Therefore 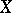 is in a natural way topologically imbedded in the space
is in a natural way topologically imbedded in the space  of maximal ideals of
of maximal ideals of  , and under the corresponding identification
, and under the corresponding identification  contains the Shilov boundary (cf. Boundary (in the theory of uniform algebras)). In the study of uniform algebras a major role is played by peak points (that is, points of
contains the Shilov boundary (cf. Boundary (in the theory of uniform algebras)). In the study of uniform algebras a major role is played by peak points (that is, points of  at which the strict maximum modulus of at least one element of
at which the strict maximum modulus of at least one element of  is attained), by multiplicative probability measures on
is attained), by multiplicative probability measures on 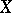 (that is, representing measures of homomorphisms from
(that is, representing measures of homomorphisms from 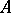 to
to 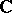 ) and by measures on
) and by measures on 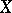 that are orthogonal to
that are orthogonal to 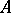 . Many concrete results relating to uniform algebras touch on the relations between these notions.
. Many concrete results relating to uniform algebras touch on the relations between these notions.
A uniform algebra is called symmetric if with each function its complex conjugate belongs to the algebra. According to the Stone–Weierstrass theorem, each symmetric uniform algebra on a compactum 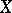 coincides with
coincides with  . The so-called anti-symmetric uniform algebras, containing no real-valued functions apart from the constants, form a kind of opposite class. A typical example is the algebra of all functions that are analytic in the open unit disc of the complex plane and continuous on its closure (the disc algebra). The Shilov–Bishop theorem: Each uniform algebra can be obtained from anti-symmetric uniform algebras by "glueing" in a certain way. Even more refined classification theorems are known. At the same time arbitrary uniform algebras do not reduce to algebras of analytic functions of the type of the disc algebra. For example, it is possible to construct a uniform algebra on a one-dimensional compactum, which coincides with its space of maximal ideals, such that all points of the compactum are peak points and at the same time only the zero element of the algebra can be zero on a non-empty open set.
. The so-called anti-symmetric uniform algebras, containing no real-valued functions apart from the constants, form a kind of opposite class. A typical example is the algebra of all functions that are analytic in the open unit disc of the complex plane and continuous on its closure (the disc algebra). The Shilov–Bishop theorem: Each uniform algebra can be obtained from anti-symmetric uniform algebras by "glueing" in a certain way. Even more refined classification theorems are known. At the same time arbitrary uniform algebras do not reduce to algebras of analytic functions of the type of the disc algebra. For example, it is possible to construct a uniform algebra on a one-dimensional compactum, which coincides with its space of maximal ideals, such that all points of the compactum are peak points and at the same time only the zero element of the algebra can be zero on a non-empty open set.
References
| [1] | T.W. Gamelin, "Uniform algebras" , Prentice-Hall (1969) |
Comments
Instead of "uniform algebra" the terminology "function algebra" is also used.
Let 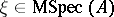 , the maximal ideal space of
, the maximal ideal space of 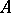 . A representing measure for
. A representing measure for 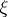 is a positive measure on
is a positive measure on 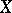 such that
such that
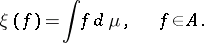 |
They exist by the Riesz representation theorem (cf. (the editorial comments to the second article) Riesz theorem). Of course, then  , so that
, so that  is a probability measure. A Jensen measure for
is a probability measure. A Jensen measure for 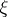 is a positive measure on
is a positive measure on 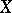 such that the Jensen inequality
such that the Jensen inequality
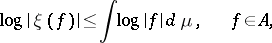 |
holds. A Jensen measure is a representing measure, and a Jensen measure for 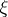 always exists.
always exists.
A measure 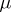 on
on 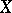 is orthogonal to
is orthogonal to 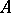 if
if 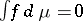 for all
for all 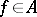 .
.
References
| [a1] | T.W. Gamelin, "Uniform algebras and Jensen measures" , Cambridge Univ. Press (1978) |
| [a2] | G.M. Leibowitz, "Lectures on complex functions algebras" , Foresman (1970) |
| [a3] | E.L. Stout, "The theory of uniform algebras" , Bogden & Quigley (1971) |
| [a4] | J. Wermer, "Banach algebras and several complex variables" , Springer (1975) |
| [a5] | I. Suciu, "Function algebras" , Ed. Acad. Romania (1973) |
| [a6] | A. Browder, "Introduction to function algebras" , Benjamin (1969) |
Uniform algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Uniform_algebra&oldid=13486