Two-dimensional manifold
A topological space each point of which has a neighbourhood which is homeomorphic to a plane or a closed half-plane. It is the class of manifolds which are easiest to visualize; it includes the sphere, the disc, the Möbius strip, the projective plane, the Klein bottle, etc.
Points with only neighbourhoods homeomorphic to a half-plane (if any) form the boundary of the manifold.
The most important class of two-dimensional manifolds are closed orientable two-dimensional manifolds, or closed surfaces. The simplest of these, the sphere  , is a surface of genus zero (cf. Genus of a surface). A surface of genus
, is a surface of genus zero (cf. Genus of a surface). A surface of genus  is obtained from
is obtained from  by removal of
by removal of  pairs of non-intersecting discs and by identifying each pair of boundary circles with boundaries of a bent cylinder (Fig. a). This process is known as glueing of handles, while the closed surface of genus
pairs of non-intersecting discs and by identifying each pair of boundary circles with boundaries of a bent cylinder (Fig. a). This process is known as glueing of handles, while the closed surface of genus  is known as a sphere with
is known as a sphere with 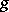 handles (Fig. b).
handles (Fig. b).

Figure: t094530a

Figure: t094530b
A wider class of two-dimensional manifolds is constituted by the compact orientable two-dimensional manifolds, or surfaces with boundary, which can be obtained from any closed surface by removing the interior points of a finite number of non-intersecting discs. Their boundaries form the boundary of the two-dimensional manifold thus generated. The genus of this manifold is considered to be the genus of the initial surface (Fig. c). A two-dimensional manifold of genus zero with boundary is a disc or a punctured disc.

Figure: t094530c

Figure: t094530d
Another class of two-dimensional manifolds are the compact non-orientable two-dimensional manifolds. They can also be closed or have a boundary. The simplest such manifold is the Möbius strip (Fig. d). It cannot be oriented, i.e. it is not possible to select on the strip a direction of rotation around each point at the same time so that these directions continuously pass into each other. Another example is the projective plane  . Each neighbourhood of any projective straight line in
. Each neighbourhood of any projective straight line in  contains the Möbius strip and for this reason
contains the Möbius strip and for this reason 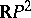 is also non-orientable. In the general case, compact non-orientable two-dimensional manifolds can be obtained from closed surfaces by elimination of the interior points of non-intersecting discs and replacing some (or all) of them by Möbius strips (Fig. eshows a Möbius strip as a crossed covering, i.e. with a self-intersection on a segment). The projective plane
is also non-orientable. In the general case, compact non-orientable two-dimensional manifolds can be obtained from closed surfaces by elimination of the interior points of non-intersecting discs and replacing some (or all) of them by Möbius strips (Fig. eshows a Möbius strip as a crossed covering, i.e. with a self-intersection on a segment). The projective plane 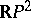 can be obtained from a sphere by replacing one of the discs by the Möbius strip. If two discs are replaced by Möbius strips, a Klein surface is obtained (Fig. f), which can also conveniently be represented as a sphere with a non-orientable handle. In general, the glueing of two Möbius strips may be replaced by the glueing of one non-orientable handle, and vice versa. On the other hand, if one end of an ordinary handle is moved along the median line of a Möbius strip, the handle will become non-orientable (Fig. g). Thus, in a non-orientable two-dimensional manifold any handle can be replaced by two Möbius strips and vice versa.
can be obtained from a sphere by replacing one of the discs by the Möbius strip. If two discs are replaced by Möbius strips, a Klein surface is obtained (Fig. f), which can also conveniently be represented as a sphere with a non-orientable handle. In general, the glueing of two Möbius strips may be replaced by the glueing of one non-orientable handle, and vice versa. On the other hand, if one end of an ordinary handle is moved along the median line of a Möbius strip, the handle will become non-orientable (Fig. g). Thus, in a non-orientable two-dimensional manifold any handle can be replaced by two Möbius strips and vice versa.

Figure: t094530e

Figure: t094530f

Figure: t094530g
Spheres with handles or with Möbius strips and, possibly, also with discs removed, account for all compact connected (consisting of one piece) two-dimensional manifolds. Non-compact two-dimensional manifolds, e.g. the plane 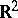 , the half-plane
, the half-plane 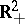 and, generally, any open proper subset of an arbitrary compact two-dimensional manifold, may have a very complicated structure. Thus, if one takes an infinite number of discs in
and, generally, any open proper subset of an arbitrary compact two-dimensional manifold, may have a very complicated structure. Thus, if one takes an infinite number of discs in  which move away to infinity and replaces them by handles or Möbius strips, the resulting two-dimensional manifold will not be an open subset of any compact two-dimensional manifold (Fig. h). Non-compact two-dimensional manifolds without boundary are said to be open.
which move away to infinity and replaces them by handles or Möbius strips, the resulting two-dimensional manifold will not be an open subset of any compact two-dimensional manifold (Fig. h). Non-compact two-dimensional manifolds without boundary are said to be open.

Figure: t094530h
One method of studying two-dimensional manifolds is the combinatorial approach, in which the manifold is regarded as being built up from convex polygons (faces), adjacent to one another by way of common edges. Triangulations (cf. Triangulation) of two-dimensional manifolds, with triangles as faces, are especially important. If two two-dimensional manifolds are triangulated, their triangulations are referred to as combinatorially equivalent if they have isomorphic subdivisions for which it is possible to establish a one-to-one correspondence between the elements under which adjacency of respective faces is preserved. Among the two-dimensional complexes (cf. Complex) of a triangulated two-dimensional manifold those are singled out for which each edge has one adjacent face (for edges on the boundary) or two faces, and for which the faces form a cycle (star) of faces sequentially adjacent to one another around each triangulation vertex (Fig. i). The cycle is closed if the vertex does not lie on the boundary (a), and is not closed if it does (b). Compactness of a two-dimensional manifold is equivalent to finiteness of the number of faces of any triangulation, while connectedness is equivalent to the possibility of connecting any two vertices by a chain of edges. In a connected two-dimensional manifold any two faces are interconnected by a chain of faces in which two adjacent faces have a common edge. Non-orientability is equivalent to the presence of a chain which comprises a Möbius strip.

Figure: t094530i
Triangulation is a convenient method for introducing invariants, i.e. characteristics which are identical in combinatorially-equivalent two-dimensional manifolds. The most important invariant is the Euler characteristic 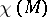 which, for a given triangulation, is equal to the number
which, for a given triangulation, is equal to the number  , where
, where 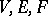 are the numbers of vertices, edges and faces of the triangulation, respectively.
are the numbers of vertices, edges and faces of the triangulation, respectively. 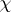 does not change under subdivision, and it follows that if
does not change under subdivision, and it follows that if 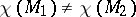 , then
, then 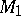 and
and  are combinatorially non-equivalent. For a sphere with
are combinatorially non-equivalent. For a sphere with 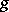 handles,
handles, 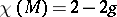 ; in particular, it is equal to 2 for spheres, to 0 for tori, to 1 for projective planes, to 0 for Klein bottles, and to
; in particular, it is equal to 2 for spheres, to 0 for tori, to 1 for projective planes, to 0 for Klein bottles, and to  for spheres with
for spheres with  Möbius strips. If the interiors of
Möbius strips. If the interiors of 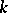 discs are eliminated from a two-dimensional manifold
discs are eliminated from a two-dimensional manifold  ,
, 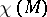 will decrease by
will decrease by  . If one assigns to a compact connected two-dimensional manifold the three numbers
. If one assigns to a compact connected two-dimensional manifold the three numbers
 |
where 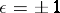 , depending on the orientability,
, depending on the orientability, 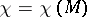 and
and 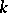 is the number of boundary components, one obtains a complete description of the two-dimensional compact manifold up to combinatorial equivalence. This is because these triplets are different for the two-dimensional manifolds described above (the sphere with handles, the sphere with Möbius strips and, possibly, with punctuations as well), while any compact connected two-dimensional manifold is combinatorially equivalent to one of these manifolds [1], [3]. A classification of open two-dimensional manifolds is also available, but it is much more involved, since the number of different surfaces in this case is uncountable [5].
is the number of boundary components, one obtains a complete description of the two-dimensional compact manifold up to combinatorial equivalence. This is because these triplets are different for the two-dimensional manifolds described above (the sphere with handles, the sphere with Möbius strips and, possibly, with punctuations as well), while any compact connected two-dimensional manifold is combinatorially equivalent to one of these manifolds [1], [3]. A classification of open two-dimensional manifolds is also available, but it is much more involved, since the number of different surfaces in this case is uncountable [5].
For a purely topological study of two-dimensional manifolds the Jordan theorem is of fundamental importance. Let  be a curve without self-intersections which connects two points on the boundary of the manifold
be a curve without self-intersections which connects two points on the boundary of the manifold 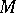 , or which is a closed curve; it is known as a section of
, or which is a closed curve; it is known as a section of  . The section
. The section 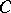 does not disconnect
does not disconnect  if any two points of
if any two points of 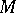 are connected by an arc which does not intersect
are connected by an arc which does not intersect 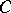 . The maximum number of sections which, together, do not disconnect
. The maximum number of sections which, together, do not disconnect  , plus one is known as the connectedness number of
, plus one is known as the connectedness number of 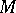 . Thus, according to Jordan's theorem, a sphere and a disc are simply connected. The connectedness number of a closed surface of genus
. Thus, according to Jordan's theorem, a sphere and a disc are simply connected. The connectedness number of a closed surface of genus 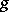 is
is  . For such a surface, a selection of
. For such a surface, a selection of 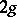 sections is available, all sections issuing from one point and being subdivided into pairs so that each pair realizes the section of one handle. Such a selection is said to be a canonical section of
sections is available, all sections issuing from one point and being subdivided into pairs so that each pair realizes the section of one handle. Such a selection is said to be a canonical section of 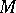 : If
: If  is cut along all these sections, a disc is obtained. The case of canonical sections of non-orientable two-dimensional manifolds (along median lines of Möbius strips) is similar. For a two-dimensional manifold with boundary, additional sections from a basic point to each component of the boundary are required. Conversely, a disc whose boundary is subdivided into segments yields a two-dimensional manifold if these segments are glued pairwise. If the glueing is effected as shown in Fig. j, an orientable two-dimensional manifold is obtained; if it is carried out as in Fig. k, the manifold will be non-orientable. (A segment
is cut along all these sections, a disc is obtained. The case of canonical sections of non-orientable two-dimensional manifolds (along median lines of Möbius strips) is similar. For a two-dimensional manifold with boundary, additional sections from a basic point to each component of the boundary are required. Conversely, a disc whose boundary is subdivided into segments yields a two-dimensional manifold if these segments are glued pairwise. If the glueing is effected as shown in Fig. j, an orientable two-dimensional manifold is obtained; if it is carried out as in Fig. k, the manifold will be non-orientable. (A segment  should be glued together with a segment
should be glued together with a segment  so that the directions of the arrows coincide.) If several segments remain unglued, a boundary is obtained.
so that the directions of the arrows coincide.) If several segments remain unglued, a boundary is obtained.

Figure: t094530j

Figure: t094530k
Jordan's theorem also makes it possible to give a topological characterization of two-dimensional manifolds. In particular, the sphere is the unique locally connected continuum containing the topological image of a circle, which is disconnected by any image of a circle and is not disconnected by any pair of points. In general, two-dimensional manifolds are distinguished from other objects in the class of locally connected continua by the fact that they are not disconnected by any pair of points and are disconnected by a sufficiently small circle (Wilder's theorem, 1949).
Since for homeomorphic two-dimensional manifolds any two triangulations are combinatorially equivalent, a combinatorial classification of two-dimensional manifolds is of a purely topological nature. While compact two-dimensional manifolds are uniquely characterized by  , other topological invariants are also of importance in the study of properties of two-dimensional manifolds. These are, first of all, the one-dimensional homology group
, other topological invariants are also of importance in the study of properties of two-dimensional manifolds. These are, first of all, the one-dimensional homology group 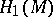 and the fundamental group
and the fundamental group 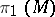 . For a closed surface of genus
. For a closed surface of genus 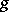 ,
,  is equal to the direct sum of
is equal to the direct sum of 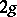 copies of the group of integers
copies of the group of integers  ;
;  pairs of a canonical section are usually taken as generators. For a non-orientable closed two-dimensional manifold with connectedness number
pairs of a canonical section are usually taken as generators. For a non-orientable closed two-dimensional manifold with connectedness number  ,
,  is the sum of
is the sum of 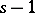 copies of the group
copies of the group  and one copy of
and one copy of  . The generating elements taken are sections of a canonical section (except one) and a path which is disoriented (after intersecting with some two-dimensional manifold this path becomes orientable). A presentation for
. The generating elements taken are sections of a canonical section (except one) and a path which is disoriented (after intersecting with some two-dimensional manifold this path becomes orientable). A presentation for 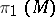 is most conveniently obtained with the aid of a canonical section: Its sections are taken as the generating elements, while the relation is obtained by traversing the boundary of the disc which results from the section. In the orientable case, one arrives at the presentation
is most conveniently obtained with the aid of a canonical section: Its sections are taken as the generating elements, while the relation is obtained by traversing the boundary of the disc which results from the section. In the orientable case, one arrives at the presentation
 |
while in the non-orientable case
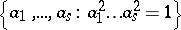 |
Note the important fact that the plane 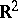 is the universal covering of any connected two-dimensional manifold without boundary (except for
is the universal covering of any connected two-dimensional manifold without boundary (except for 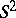 and
and  ), while the corresponding monodromy group is realized by motions of the Euclidean or the Lobachevskii plane. Thus, a torus is obtained by identification of all points in the plane differing from one another by
), while the corresponding monodromy group is realized by motions of the Euclidean or the Lobachevskii plane. Thus, a torus is obtained by identification of all points in the plane differing from one another by 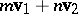 , where
, where 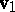 and
and 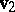 are two given vectors and
are two given vectors and 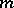 and
and  are integers. In applications, branched coverings are also of importance. Consider a mapping
are integers. In applications, branched coverings are also of importance. Consider a mapping 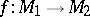 , where
, where 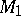 and
and  are closed triangulated two-dimensional manifolds, which linearly maps each face of
are closed triangulated two-dimensional manifolds, which linearly maps each face of 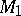 into some face
into some face 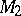 , and where for each edge
, and where for each edge  in
in  the two adjacent faces are mapped into different faces adjacent to the edge
the two adjacent faces are mapped into different faces adjacent to the edge 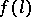 in
in 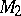 . For each point
. For each point  other than a vertex, it is possible to find a neighbourhood in
other than a vertex, it is possible to find a neighbourhood in  which is one-to-one transformed by
which is one-to-one transformed by  into a neighbourhood of the point
into a neighbourhood of the point 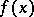 in
in  . If, for a vertex
. If, for a vertex  of
of 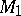 , one cyclically traverses all the adjoining faces, the respective faces in
, one cyclically traverses all the adjoining faces, the respective faces in 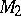 will cyclically traverse around
will cyclically traverse around  in
in 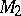 an integral number,
an integral number, 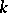 , of times. If
, of times. If 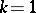 ,
,  is an ordinary point; if
is an ordinary point; if  ,
,  is a branch point, and
is a branch point, and  is the multiplicity of branching at
is the multiplicity of branching at  . If
. If 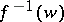 for
for  contains no branch points,
contains no branch points, 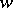 is also called an ordinary point. Since the pre-images of nearby ordinary points in
is also called an ordinary point. Since the pre-images of nearby ordinary points in 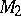 consist of an equal number of points, by continuity this number will be the same for all ordinary points. It is called the number of covering sheets. This number
consist of an equal number of points, by continuity this number will be the same for all ordinary points. It is called the number of covering sheets. This number 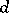 is equal, for an orientable two-dimensional manifold, to the degree of the mapping (cf. Degree of a mapping)
is equal, for an orientable two-dimensional manifold, to the degree of the mapping (cf. Degree of a mapping) 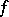 (in the non-orientable case, it must be reduced modulo 2). If
(in the non-orientable case, it must be reduced modulo 2). If  contains branch points with multiplicities
contains branch points with multiplicities 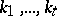 , then
, then 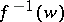 contains
contains 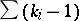 fewer points than for an ordinary point (here, the summation is over all the branch points in
fewer points than for an ordinary point (here, the summation is over all the branch points in 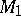 ). Since the number of vertices,
). Since the number of vertices, 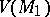 , is
, is  less than
less than 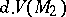 , while the numbers of edges and faces are given by
, while the numbers of edges and faces are given by 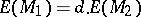 and
and 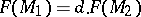 , one has
, one has
 |
This is the Riemann–Hurwitz formula.
From the point of view of differential geometry, two-dimensional manifolds can be regarded as smooth manifolds with supplementary structures (e.g. metric, connections, etc.), or else as imbedded (possibly with self-intersections) into Euclidean spaces. A smooth two-dimensional manifold can be triangulated so that the edges are smooth arcs and all angles are non-zero (Cairns' theorem, 1934). Here, combinatorially-equivalent triangulations correspond to diffeomorphic two-dimensional manifolds, and vice versa. Thus, the classification of two-dimensional manifolds holds for smooth two-dimensional manifolds as well. An example of a theorem relating the topological characteristics of a two-dimensional manifold with its differential-geometric properties is the Gauss–Bonnet theorem [3]: The integral of the curvature of a closed surface (more exactly, of the Gaussian curvature defined by some Riemannian connection, which can always be defined on a smooth two-dimensional manifold) is equal to  . This fact, as well as its interpretation using the so-called Gauss mapping (in particular, the spherical map) into a Grassmann manifold, if the manifold is immersed in a Euclidean space, is generalized in the theory of characteristic classes (cf. Characteristic class). Another theorem, which is also one of the sources of this theory, states that the sum of the indices (cf. Index) of the singular points of any vector field on a closed surface is equal to
. This fact, as well as its interpretation using the so-called Gauss mapping (in particular, the spherical map) into a Grassmann manifold, if the manifold is immersed in a Euclidean space, is generalized in the theory of characteristic classes (cf. Characteristic class). Another theorem, which is also one of the sources of this theory, states that the sum of the indices (cf. Index) of the singular points of any vector field on a closed surface is equal to 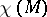 .
.
Two-dimensional manifolds play an important part in the theory of functions of a complex variable. Here, such manifolds have complex structures, i.e. the local coordinates in neighbourhoods of points are related by analytic functions, and are known as Riemann surfaces (cf. Riemann surface) [4]. They are all orientable. Closed Riemann surfaces are geometric models of complex algebraic curves (cf. Algebraic curve). A complex structure on a two-dimensional manifold is not uniquely defined by its differential-topological structure. For example, on a surface of genus 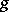 the complex structures form a continuum of dimension
the complex structures form a continuum of dimension 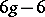 (Teichmüller's theorem, 1940) if
(Teichmüller's theorem, 1940) if 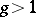 (cf. Teichmüller space).
(cf. Teichmüller space).
Special requirements are sometimes imposed on the definition of a two-dimensional manifold, viz., that as a topological space it be Hausdorff or that it have a countable base. The latter condition, in particular, is essential for the manifold to be triangulable: Non-triangulable two-dimensional Hausdorff manifolds exist (cf. Prüfer surface).
References
| [1] | P.S. Aleksandrov, V.A. Efremovich, "Outline of fundamental concepts in topology" , Moscow-Leningrad (1936) (In Russian) |
| [2] | D. Hilbert, S.E. Cohn-Vossen, "Geometry and the imagination" , Chelsea (1956) (Translated from German) |
| [3] | I.Ya. Bakel'man, A.L. Verner, B.E. Kantor, "Introduction to geometry "in the large" " , Moscow (1973) (In Russian) |
| [4] | G. Springer, "Introduction to Riemann surfaces" , Addison-Wesley (1957) pp. Chapt.10 |
| [5] | S. [S. Stoilov] Stoilow, "Leçons sur les principes topologiques de la théorie des fonctions analytiques" , Gauthier-Villars (1938) |
Comments
References
| [a1] | M.W. Hirsch, "Differential topology" , Springer (1976) pp. Chapt. 6 |
| [a2] | E.M. Moise, "Geometric topology in dimensions 2 and 3" , Springer (1977) |
| [a3] | O. Forster, "Lectures on Riemann surfaces" , Springer (1977) (Translated from German) |
| [a4] | Yu. Borisovich, N. Bliznyakov, Ya. Izrailevich, T. Fomenko, "Introduction to topology" , Kluwer (1993) (Translated from Russian) |
| [a5] | R.S. Millman, G.D. Parker, "Elements of differential geometry" , Prentice-Hall (1977) pp. 26 |
Two-dimensional manifold. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Two-dimensional_manifold&oldid=18443