Triple
monad, on a category 
A monoid in the category of all endomorphism functors on  . In other words, a triple on a category
. In other words, a triple on a category  is a covariant functor
is a covariant functor  endowed with natural transformations
endowed with natural transformations  and
and  (here
(here  denotes the identity functor on
denotes the identity functor on  ) such that the following diagrams are commutative:
) such that the following diagrams are commutative:
 |
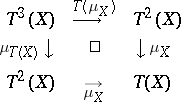 |
A triple is sometimes called a standard construction, cf. [2].
For any pair of adjoint functors  and
and  (see Adjoint functor) with unit and co-unit of adjunction
(see Adjoint functor) with unit and co-unit of adjunction 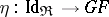 and
and 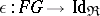 , respectively, the functor
, respectively, the functor  endowed with
endowed with  and
and  is a triple on
is a triple on  . Conversely, for any triple
. Conversely, for any triple 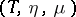 there exist pairs of adjoint functors
there exist pairs of adjoint functors  and
and 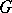 such that
such that  , and the transformations
, and the transformations 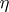 and
and 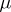 are obtained from the unit and co-unit of the adjunction in the manner described above. The different such decompositions of a triple may form a proper class. In this class there is a smallest element (the Kleisli construction) and a largest element (the Eilenberg–Moore construction).
are obtained from the unit and co-unit of the adjunction in the manner described above. The different such decompositions of a triple may form a proper class. In this class there is a smallest element (the Kleisli construction) and a largest element (the Eilenberg–Moore construction).
Examples.
1) In the category of sets, the functor which sends an arbitrary set to the set of all its subsets has the structure of a triple. Each set  is naturally imbedded in the set of its subsets via singleton sets, and to each set of subsets of
is naturally imbedded in the set of its subsets via singleton sets, and to each set of subsets of  one associates the union of these subsets.
one associates the union of these subsets.
2) In the category of sets, every representable functor  carries a triple: The mapping
carries a triple: The mapping  associates to each
associates to each 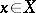 the constant function
the constant function  with value
with value  ; the mapping
; the mapping  associates to each function of two variables its restriction to the diagonal.
associates to each function of two variables its restriction to the diagonal.
3) In the category of topological spaces, each topological group  , with unit
, with unit  , enables one to define a functor
, enables one to define a functor 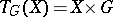 that carries a triple: Each element
that carries a triple: Each element  is taken to the element
is taken to the element 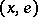 and the mapping
and the mapping 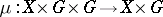 is defined by
is defined by  .
.
4) In the category of modules over a commutative ring 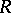 , each (associative, unital)
, each (associative, unital)  -algebra
-algebra 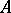 gives rise to a triple structure on the functor
gives rise to a triple structure on the functor  , in a manner similar to Example 3).
, in a manner similar to Example 3).
References
| [1] | J.F. Adams, "Infinite loop spaces" , Princeton Univ. Press (1978) |
| [2] | R. Godement, "Topologie algébrique et théorie des faisceaux" , Hermann (1958) |
| [3] | M.Sh. Tsalenko, E.G. Shul'geifer, "Categories" J. Soviet Math. , 7 : 4 (1977) pp. 532–586 Itogi Nauk. i Tekhn. Algebra Topol. Geom. , 13 (1975) pp. 51–148 |
| [4] | S. MacLane, "Categories for the working mathematician" , Springer (1971) |
| [5] | E.G. Manes, "Algebraic theories" , Springer (1976) |
Comments
The non-descriptive name "triple" for this concept has now largely been superseded by "monad" , although there is an obstinate minority of category-theorists who continue to use it. A comonad (or cotriple) on a category  is a monad on
is a monad on  ; in other words, it is a functor
; in other words, it is a functor 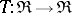 equipped with natural transformations
equipped with natural transformations  and
and  satisfying the duals of the commutative diagrams above. Every adjoint pair of functors (
satisfying the duals of the commutative diagrams above. Every adjoint pair of functors ( ) gives rise to a comonad structure on the composite
) gives rise to a comonad structure on the composite  , as well as a monad structure on
, as well as a monad structure on  .
.
An important example of a functor which carries a comonad structure is 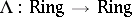 ,
,  , or, equivalently, the functor of big Witt vectors, cf.
, or, equivalently, the functor of big Witt vectors, cf.  -ring; Witt vector. A special case of the natural transformation
-ring; Witt vector. A special case of the natural transformation  occurs in algebraic number theory as the Artin–Hasse exponential, [a5].
occurs in algebraic number theory as the Artin–Hasse exponential, [a5].
Monads in the category of sets can be equivalently described by sets  of
of  -ary operations for each cardinal number (or set)
-ary operations for each cardinal number (or set)  ;
;  gives the projection operations
gives the projection operations  , and
, and 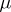 gives the rules for composing operations. See [5] or [a1]. This approach extends to monads in arbitrary categories, but it has not proved useful in general, as it has in or near sets.
gives the rules for composing operations. See [5] or [a1]. This approach extends to monads in arbitrary categories, but it has not proved useful in general, as it has in or near sets.
Of the two canonical ways of constructing an adjunction from a given monad, mentioned in the main article above, the Eilenberg–Moore construction (or category of 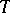 -algebras) is by far the more important. Given a monad
-algebras) is by far the more important. Given a monad 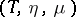 on a category
on a category  , a
, a  -algebra in
-algebra in  is a pair
is a pair 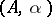 where
where  is a morphism such that
is a morphism such that
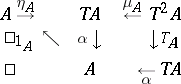 |
commutes. A homomorphism of 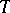 -algebras
-algebras  is a morphism
is a morphism  in
in  such that
such that
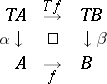 |
commutes; thus, one has a category  of
of 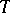 -algebras, with an evident forgetful functor
-algebras, with an evident forgetful functor  . The functor
. The functor  has a left adjoint
has a left adjoint  , which sends an object
, which sends an object  of
of  to the
to the 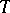 -algebra
-algebra 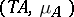 , and the monad induced by the adjunction (
, and the monad induced by the adjunction ( ) is the one originally given.
) is the one originally given.
Now the Kleisli category of  is just the full subcategory of
is just the full subcategory of  on the objects
on the objects  : the category of free algebras (cf. also Category).
: the category of free algebras (cf. also Category).
For a monad  on
on  , in the Kleisli construction the category
, in the Kleisli construction the category 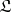 has as objects the objects of
has as objects the objects of  , and as hom-sets the sets
, and as hom-sets the sets
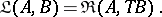 |
The composition rule for  assigns to
assigns to  and
and  the
the  -composite:
-composite:
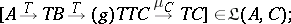 |
as identity mapping 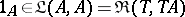 one uses the
one uses the  -morphism
-morphism  .
.
An adjoint pair  ,
, 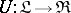 is obtained by setting
is obtained by setting 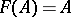 for
for 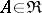 ,
,
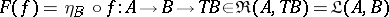 |
for  ,
,  for
for  , and
, and  for
for  .
.
Then 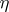 will serve as unit for the adjunction, while the co-unit
will serve as unit for the adjunction, while the co-unit  is given by
is given by
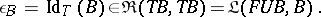 |
Co-algebras are defined in the same manner. In practice, co-algebras very often occur superposed on algebras; a comonad 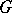 will be constructed on a category of algebras of some sort,
will be constructed on a category of algebras of some sort,  , leading to the category
, leading to the category 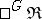 of bi-algebras. An important class of cases involves a monad
of bi-algebras. An important class of cases involves a monad 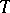 and a cotriple
and a cotriple 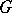 on the same category
on the same category  . There is a standard lifting of
. There is a standard lifting of 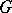 to a cotriple
to a cotriple  on
on 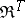 . A "TG-bi-algebraTG-bi-algebra" means an object of
. A "TG-bi-algebraTG-bi-algebra" means an object of 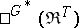 ; the reverse order is also possible, but rarely occurs, and the objects would not be called bi-algebras.
; the reverse order is also possible, but rarely occurs, and the objects would not be called bi-algebras.
For the role of comonads in (algebraic) cohomology theories see Cohomology of algebras and [a2], [a3]; particularly [a2] for explicit interpretation.
An adjunction is said to be monadic (or monadable) if the Eilenberg–Moore construction applied to the monad it induces yields an adjunction equivalent to the original one. Many important examples of adjunctions are monadic; for example, for any variety of universal algebras, the forgetful functor from the variety to the category of sets and its left adjoint (the free algebra functor) form a monadic adjunction.
A monad 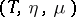 is said to be idempotent if
is said to be idempotent if 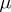 is an isomorphism. In this case it can be shown that any
is an isomorphism. In this case it can be shown that any 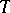 -algebra structure
-algebra structure  on an object
on an object 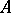 is necessarily a two-sided inverse for
is necessarily a two-sided inverse for 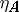 , and hence that
, and hence that  is isomorphic to the full subcategory
is isomorphic to the full subcategory 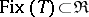 consisting of all objects
consisting of all objects 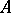 such that
such that  is an isomorphism.
is an isomorphism.  is a reflective subcategory of
is a reflective subcategory of 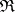 , the left adjoint to the inclusion being given by
, the left adjoint to the inclusion being given by 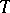 itself. Conversely, for any reflective subcategory of
itself. Conversely, for any reflective subcategory of  , the monad on
, the monad on 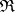 induced by the inclusion and its left adjoint is idempotent; thus, the adjunctions corresponding to reflective subcategories are always monadic.
induced by the inclusion and its left adjoint is idempotent; thus, the adjunctions corresponding to reflective subcategories are always monadic.
References
| [a1] | M. Barr, C. Wells, "Toposes, monads, and theories" , Springer (1985) |
| [a2] | J.W. Duskin, " -torsors and the interpretation of "monad" cohomology" Proc. Nat. Acad. Sci. USA , 71 (1974) pp. 2554–2557 -torsors and the interpretation of "monad" cohomology" Proc. Nat. Acad. Sci. USA , 71 (1974) pp. 2554–2557 |
| [a3] | J.W. Duskin, "Simplicial methods and the interpretation of "monad" cohomology" Mem. Amer. Math. Soc. , 3 (1975) |
| [a4] | J. Adamek, H. Herrlich, G.E. Strecker, "Abstract and concrete categories" , Wiley (Interscience) (1990) |
| [a5] | M. Hazewinkel, "Formal groups" , Acad. Press (1978) pp. Sects. 14.5; 14.6, E2 |
| [a6] | H. Appelgate (ed.) et al. (ed.) , Seminar on monads and categorical homology theory ETH 1966/7 , Lect. notes in math. , 80 , Springer (1969) |
| [a7] | S. Eilenberg, J.C. Moore, "Adjoint functors and monads" Ill. J. Math. , 9 (1965) pp. 381–398 |
| [a8] | S. Eilenberg (ed.) et al. (ed.) , Proc. conf. categorical algebra (La Jolla, 1965) , Springer (1966) |
Triple. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Triple&oldid=16681