Difference between revisions of "Transition function"
(MSC|60J35 Category:Markov processes) |
(refs format) |
||
| Line 23: | Line 23: | ||
for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376042.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376043.png" /> from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376044.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376045.png" /> from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376046.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376047.png" /> is called a transition density. | for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376042.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376043.png" /> from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376044.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376045.png" /> from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376046.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376047.png" /> is called a transition density. | ||
| − | Under very general conditions (cf. | + | Under very general conditions (cf. {{Cite|N}}, {{Cite|GS}}), the transition function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376048.png" /> can be related to a Markov process <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376049.png" /> for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376050.png" /> (in the case of a Markov transition function, this process does not terminate, i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376051.png" /> <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376052.png" />-a.s.). On the other hand, the Markov property for a random process enables one, as a rule, to put the process into correspondence with a transition function {{Cite|K}}. |
Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376053.png" /> be homogeneous in the sense that the set of values of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376054.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376055.png" /> from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376056.png" /> forms a semi-group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376057.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376058.png" /> under addition (for example, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376059.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376060.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376061.png" />). If, moreover, the transition function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376062.png" /> depends only on the difference <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376063.png" />, i.e. if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376064.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376065.png" /> is a function of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376066.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376067.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376068.png" /> satisfying the corresponding form of conditions a)–d), then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376069.png" /> is called a homogeneous transition function. The latter name is also given to a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376070.png" /> for which (*) takes the form | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376053.png" /> be homogeneous in the sense that the set of values of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376054.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376055.png" /> from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376056.png" /> forms a semi-group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376057.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376058.png" /> under addition (for example, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376059.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376060.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376061.png" />). If, moreover, the transition function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376062.png" /> depends only on the difference <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376063.png" />, i.e. if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376064.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376065.png" /> is a function of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376066.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376067.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376068.png" /> satisfying the corresponding form of conditions a)–d), then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376069.png" /> is called a homogeneous transition function. The latter name is also given to a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093760/t09376070.png" /> for which (*) takes the form | ||
| Line 34: | Line 34: | ||
====References==== | ====References==== | ||
| − | + | {| | |
| − | + | |valign="top"|{{Ref|N}}|| J. Neveu, "Bases mathématiques du calcul des probabilités" , Masson (1970) {{MR|0272004}} {{ZBL|0203.49901}} | |
| − | + | |- | |
| + | |valign="top"|{{Ref|GS}}|| I.I. Gihman, A.V. Skorohod, "The theory of stochastic processes" , '''2''' , Springer (1975) (Translated from Russian) {{MR|0375463}} {{ZBL|0305.60027}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|K}}|| S.E. Kuznetsov, "Any Markov process in a Borel space has a transition function" ''Theory Probab. Appl.'' , '''25''' : 2 (1980) pp. 384–388 ''Teor. Veroyatnost. i ee Primenen.'' , '''25''' : 2 (1980) pp. 389–393 {{MR|0572574}} {{ZBL|0456.60077}} {{ZBL|0431.60071}} | ||
| + | |} | ||
====Comments==== | ====Comments==== | ||
| Line 42: | Line 46: | ||
====References==== | ====References==== | ||
| − | + | {| | |
| + | |valign="top"|{{Ref|DM}}|| C. Dellacherie, P.A. Meyer, "Probabilities and potential" , '''1–3''' , North-Holland (1978–1988) pp. Chapts. XII-XVI (Translated from French) {{MR|0939365}} {{MR|0898005}} {{MR|0727641}} {{MR|0745449}} {{MR|0566768}} {{MR|0521810}} {{ZBL|0716.60001}} {{ZBL|0494.60002}} {{ZBL|0494.60001}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|S}}|| M.J. Sharpe, "General theory of Markov processes" , Acad. Press (1988) {{MR|0958914}} {{ZBL|0649.60079}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|AM}}|| S. Albeverio, Z.M. Ma, "A note on quasicontinuous kernels representing quasilinear positive maps" ''Forum Math.'' , '''3''' (1991) pp. 389–400 | ||
| + | |} | ||
Revision as of 14:18, 31 May 2012
transition probability
2020 Mathematics Subject Classification: Primary: 60J35 [MSN][ZBL]
A family of measures used in the theory of Markov processes for determining the distribution at future instants from known states at previous times. Let a measurable space  be such that the
be such that the 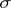 -algebra
-algebra  contains all one-point subsets from
contains all one-point subsets from  , and let
, and let 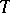 be a subset of the real line
be a subset of the real line  . A function
. A function  given for
given for 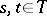 ,
, 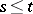 ,
,  and
and  is called a transition function for
is called a transition function for  if: a) for given
if: a) for given  ,
,  and
and 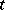 , it is a measure on
, it is a measure on 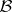 , with
, with 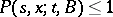 ; b) for given
; b) for given  ,
,  and
and 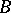 , it is a
, it is a  -measurable function of the point
-measurable function of the point  ; c)
; c)  and for all limit points
and for all limit points  of
of 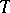 from the right in the topology of
from the right in the topology of 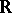 ,
,
 |
and d) for all 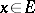 ,
,  and
and 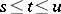 from
from  , the Kolmogorov–Chapman equation is fulfilled:
, the Kolmogorov–Chapman equation is fulfilled:
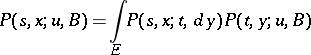 | (*) |
(in some cases, requirement c) may be omitted or weakened). A transition function is called a Markov transition function if 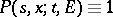 , and a subMarkov transition function otherwise. If
, and a subMarkov transition function otherwise. If 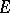 is at most countable, then the transition function is specified by means of the matrix of transition probabilities
is at most countable, then the transition function is specified by means of the matrix of transition probabilities
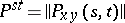 |
(see Transition probabilities; Matrix of transition probabilities). It often happens that for any admissible  ,
,  and
and 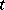 the measure
the measure 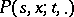 has a density
has a density  with respect to a certain measure. If in this case the following form of equation (*) is satisfied:
with respect to a certain measure. If in this case the following form of equation (*) is satisfied:
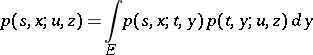 |
for any  and
and  from
from 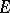 and
and 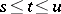 from
from 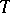 , then
, then 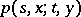 is called a transition density.
is called a transition density.
Under very general conditions (cf. [N], [GS]), the transition function 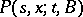 can be related to a Markov process
can be related to a Markov process 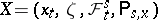 for which
for which  (in the case of a Markov transition function, this process does not terminate, i.e.
(in the case of a Markov transition function, this process does not terminate, i.e. 
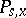 -a.s.). On the other hand, the Markov property for a random process enables one, as a rule, to put the process into correspondence with a transition function [K].
-a.s.). On the other hand, the Markov property for a random process enables one, as a rule, to put the process into correspondence with a transition function [K].
Let  be homogeneous in the sense that the set of values of
be homogeneous in the sense that the set of values of  for
for  from
from 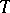 forms a semi-group
forms a semi-group  in
in 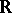 under addition (for example,
under addition (for example, 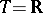 ,
, 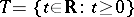 ,
, 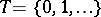 ). If, moreover, the transition function
). If, moreover, the transition function  depends only on the difference
depends only on the difference  , i.e. if
, i.e. if 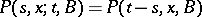 , where
, where 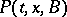 is a function of
is a function of 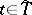 ,
, 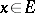 ,
,  satisfying the corresponding form of conditions a)–d), then
satisfying the corresponding form of conditions a)–d), then  is called a homogeneous transition function. The latter name is also given to a function
is called a homogeneous transition function. The latter name is also given to a function 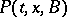 for which (*) takes the form
for which (*) takes the form
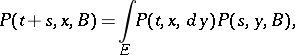 |
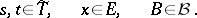 |
For certain purposes (such as regularizing transition functions) it is necessary to extend the definition. For example, one takes as given a family of measurable spaces 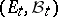 ,
, 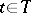 , while a transition function with respect to this family is defined as a function
, while a transition function with respect to this family is defined as a function 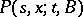 , where
, where 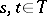 ,
, 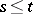 ,
, 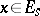 ,
, 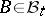 , that satisfies a suitable modification of conditions a)–d).
, that satisfies a suitable modification of conditions a)–d).
References
| [N] | J. Neveu, "Bases mathématiques du calcul des probabilités" , Masson (1970) MR0272004 Zbl 0203.49901 |
| [GS] | I.I. Gihman, A.V. Skorohod, "The theory of stochastic processes" , 2 , Springer (1975) (Translated from Russian) MR0375463 Zbl 0305.60027 |
| [K] | S.E. Kuznetsov, "Any Markov process in a Borel space has a transition function" Theory Probab. Appl. , 25 : 2 (1980) pp. 384–388 Teor. Veroyatnost. i ee Primenen. , 25 : 2 (1980) pp. 389–393 MR0572574 Zbl 0456.60077 Zbl 0431.60071 |
Comments
For additional references see also Markov chain; Markov process.
References
| [DM] | C. Dellacherie, P.A. Meyer, "Probabilities and potential" , 1–3 , North-Holland (1978–1988) pp. Chapts. XII-XVI (Translated from French) MR0939365 MR0898005 MR0727641 MR0745449 MR0566768 MR0521810 Zbl 0716.60001 Zbl 0494.60002 Zbl 0494.60001 |
| [S] | M.J. Sharpe, "General theory of Markov processes" , Acad. Press (1988) MR0958914 Zbl 0649.60079 |
| [AM] | S. Albeverio, Z.M. Ma, "A note on quasicontinuous kernels representing quasilinear positive maps" Forum Math. , 3 (1991) pp. 389–400 |
Transition function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Transition_function&oldid=24666