Transcendency, measure of
transcendence measure
A function characterizing the deviation of a given transcendental number from a set of algebraic numbers of bounded degree and bounded height under a change of bounds on these parameters. For a transcendental number  and natural numbers
and natural numbers  and
and  , the measure of transcendency is
, the measure of transcendency is
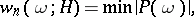 |
where the minimum is taken over all non-zero integer polynomials of degree not exceeding  and height not exceeding
and height not exceeding  . It follows from Dirichlet's "box" principle (cf. Dirichlet principle) that the following always holds:
. It follows from Dirichlet's "box" principle (cf. Dirichlet principle) that the following always holds:
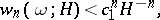 |
where  depends only on
depends only on  . In many cases it is possible to obtain not only a proof of the transcendency of a number
. In many cases it is possible to obtain not only a proof of the transcendency of a number  but also a lower bound for the measure of transcendency in terms of the degree, and logarithmic or exponential functions of
but also a lower bound for the measure of transcendency in terms of the degree, and logarithmic or exponential functions of  and
and 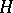 . For example, Hermite's method of proof of transcendency of
. For example, Hermite's method of proof of transcendency of  enables one to obtain the inequality
enables one to obtain the inequality
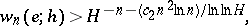 |
where 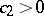 is an absolute constant and
is an absolute constant and 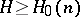 . For any fixed
. For any fixed  and
and 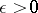 ,
,
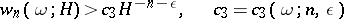 |
for almost-all (in the sense of Lebesgue) real numbers 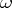 (see Mahler problem). Transcendental numbers can be classified on the basis of the difference in asymptotic behaviour of
(see Mahler problem). Transcendental numbers can be classified on the basis of the difference in asymptotic behaviour of 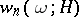 under unrestricted variation of
under unrestricted variation of  and
and 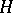 (see [3]).
(see [3]).
References
| [1] | A.O. Gel'fond, "Transcendental and algebraic numbers" , Dover, reprint (1960) (Translated from Russian) |
| [2] | P.L. Cijsouw, "Transcendence measures" , Univ. Amsterdam (1972) (Dissertation) |
| [3] | A. Baker, "Transcendental number theory" , Cambridge Univ. Press (1975) |
Comments
References
| [a1] | A.B. Shidlovskii, "Transcendental numbers" , de Gruyter (1989) (Translated from Russian) |
Transcendency, measure of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Transcendency,_measure_of&oldid=17605