Torus knot
of type 
A curve in  that in cylindrical coordinates
that in cylindrical coordinates  is given by the equations
is given by the equations
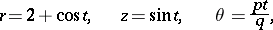 |
where  . Here
. Here  and
and  are coprime natural numbers. The torus knot lies on the surface of the unknotted torus
are coprime natural numbers. The torus knot lies on the surface of the unknotted torus  , intersecting the meridians of the torus at
, intersecting the meridians of the torus at  points and the parallels at
points and the parallels at 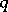 points. The torus knots of types
points. The torus knots of types 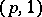 and
and  are trivial. The simplest non-trivial torus knot is the trefoil (Fig. a), which is of type
are trivial. The simplest non-trivial torus knot is the trefoil (Fig. a), which is of type  . The group of the torus knot of type
. The group of the torus knot of type 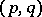 has a presentation
has a presentation  :
: 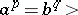 , and the Alexander polynomial is given by
, and the Alexander polynomial is given by
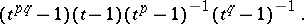 |
All torus knots are Neuwirth knots (cf. Neuwirth knot). The genus of a torus knot is  .
.
A second construction of a torus knot uses the singularity at the origin of the algebraic hypersurface
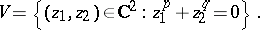 |
If  and
and 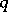 are coprime, then the intersection of
are coprime, then the intersection of  with a sufficiently small sphere
with a sufficiently small sphere  is a knot in
is a knot in  equivalent to the torus knot of type
equivalent to the torus knot of type  . In the case when
. In the case when 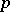 and
and 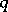 are not coprime, this intersection also lies on an unknotted torus
are not coprime, this intersection also lies on an unknotted torus  , but consists of several components. The link so obtained is called the torus link of type
, but consists of several components. The link so obtained is called the torus link of type  (cf. Fig. b, where
(cf. Fig. b, where  ,
,  ).
).

Figure: t093360a

Figure: t093360b
References
| [1] | R.H. Crowell, R.H. Fox, "Introduction to knot theory" , Ginn (1963) |
| [2] | J. Milnor, "Singular points of complex hypersurfaces" , Princeton Univ. Press (1968) |
Comments
See also Knot theory.
References
| [a1] | D. Rolfsen, "Knots and links" , Publish or Perish (1976) |
Torus knot. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Torus_knot&oldid=11550