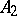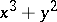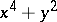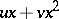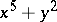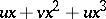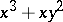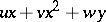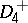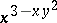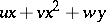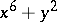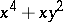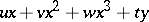Thom catastrophes
Singularities of differentiable mappings, whose classification was announced by R. Thom [1] in terms of their gradient dynamical systems and the analogous list of critical points of codimension  (cf. Critical point) of differentiable functions. The original formulation of Thom's result is that a generic four-parameter family of functions is stable, and in the neighbourhood of a critical point it behaves, up to sign and change of variable, like one of seven cases (cf. Table).'
(cf. Critical point) of differentiable functions. The original formulation of Thom's result is that a generic four-parameter family of functions is stable, and in the neighbourhood of a critical point it behaves, up to sign and change of variable, like one of seven cases (cf. Table).'
<tbody> </tbody>
|
The germs (cf. Germ) corresponding to the Thom catastrophes are finitely determined (specifically,  -determined: in appropriate coordinates they correspond to polynomials in two variables of degrees
-determined: in appropriate coordinates they correspond to polynomials in two variables of degrees  ).
).
The codimension  serves as a measure of the complexity of a critical point. Any small perturbation of a function
serves as a measure of the complexity of a critical point. Any small perturbation of a function  of
of  leads to a function with at most
leads to a function with at most  complex critical points. The codimension of a singularity (that is, of a germ
complex critical points. The codimension of a singularity (that is, of a germ  such that
such that 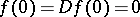 ) is the number
) is the number 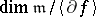 , where
, where 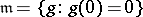 and
and  is the ideal generated by the germs
is the ideal generated by the germs  . For example, if
. For example, if 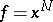 , then
, then  , and the residue classes of
, and the residue classes of 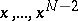 form a basis of
form a basis of  , so that
, so that  . The inequality
. The inequality  , holds, where
, holds, where  is the corank of the Hessian
is the corank of the Hessian 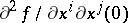 . Hence, in particular, if
. Hence, in particular, if  , then
, then 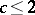 .
.
Finite determination (sufficiency) of a germ, roughly speaking, means that it is determined, up to smooth change of coordinates, by its jets (cf. Jet). More precisely, a germ  is said to be
is said to be  -determined if every germ
-determined if every germ  with the same
with the same  -jet (that is, the same Taylor series up to order
-jet (that is, the same Taylor series up to order  ) as
) as  is right equivalent to
is right equivalent to 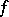 (i.e.
(i.e.  where
where 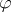 is the germ at
is the germ at  of a diffeomorphism; cf. [2]). A germ is finitely determined if and only if it has finite codimension. In particular, if
of a diffeomorphism; cf. [2]). A germ is finitely determined if and only if it has finite codimension. In particular, if  , then
, then 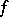 is
is 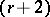 -determined (whence
-determined (whence  -determined for
-determined for  ).
).
The Thom catastrophes, in contrast to the case of general position, are degenerate singularities (that is, the Hessian is degenerate at them), and they can be removed by a small perturbation, as mentioned above. However, in many cases of practical importance, and also theoretically, one is interested not in an individual object, but in a collection of them, depending on some "control" parameters. Degenerate singularities which are removable for each fixed value of the parameters may be removable for the collection as a whole. (Stability of Thom catastrophes may also be considered in this sense.) But then the natural object of study is not the singularity itself, but a collection (a deformation of the singularity) in which it is non-removable (or disintegrates, or "bifurcates" ) under a change of parameters. It turns out that in many cases the study of all possible deformations can be reduced to the study of a single one, which is in a certain sense so big that all the others can be obtained from it. Such deformations are called versal and they, in turn, can be obtained from a universal (or miniversal) deformation, which is characterized by having least possible dimension of its parameter space. The most important result here is Mather's theorem: A singularity  has a universal deformation if and only if its codimension is finite.
has a universal deformation if and only if its codimension is finite.
A deformation 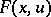 ,
,  ,
, 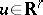 , of a germ
, of a germ 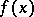 ,
,  , is given by a formula
, is given by a formula
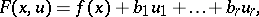 |
where 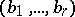 is an arbitrary collection of representative elements of a basis of the space
is an arbitrary collection of representative elements of a basis of the space 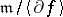 . Thom catastrophes correspond to deformations with at most four parameters.
. Thom catastrophes correspond to deformations with at most four parameters.
Important for applications is the so-called bifurcation set, or singular set, 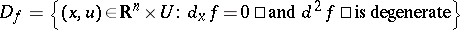 ; its projection to the
; its projection to the  -space, the set
-space, the set  , is called the catastrophe set. It lies in the control space and hence is "observable" , and all "discontinuities" or "catastrophes" originate from it. Fig.1a, Fig.1b and Fig.1c illustrate the cases corresponding to
, is called the catastrophe set. It lies in the control space and hence is "observable" , and all "discontinuities" or "catastrophes" originate from it. Fig.1a, Fig.1b and Fig.1c illustrate the cases corresponding to  .
.

Figure: t092650a

Figure: t092650b

Figure: t092650c
References
| [1] | R. Thom, "Topological models in biology" Topology , 8 (1969) pp. 313–335 |
| [2] | P. Bröcker, L. Lander, "Differentiable germs and catastrophes" , Cambridge Univ. Press (1975) |
| [3] | T. Poston, I. Stewart, "Catastrophe theory and its applications" , Pitman (1978) |
Comments
References
| [a1] | R. Thom, "Structural stability and morphogenesis" , Benjamin (1976) (Translated from French) |
| [a2] | R. Thom, "Mathematical models of morphogenesis" , Wiley (1983) (Translated from French) |
| [a3] | V.I. Arnol'd, "Catastrophe theory" , Springer (1984) (Translated from Russian) |
| [a4] | E.C. Zeeman, "Catastrophe theory" , Addison-Wesley (1977) |
Thom catastrophes. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Thom_catastrophes&oldid=18262