Ternary field
planar ternary ring
A set 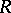 with two special elements,
with two special elements,  and
and 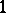 , provided with a ternary operation
, provided with a ternary operation 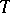 satisfying:
satisfying:
A)  for all
for all 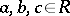 ;
;
B)  for all
for all 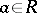 ;
;
C) if  ,
, 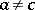 , then there is a unique
, then there is a unique 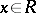 such that
such that  ;
;
D) if 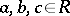 , then there is a unique
, then there is a unique 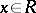 such that
such that 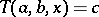 ;
;
E) if 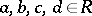 ,
, 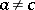 , then there are unique
, then there are unique 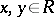 such that
such that  and
and 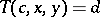 .
.
Ternary fields were introduced in [a1] for the purpose of coordinatizing arbitrary, not necessarily Desarguesian, projective planes (cf. Desargues assumption; Desargues geometry; Projective plane). Slight variations of the original definition were given in [a2] and [a3], which is followed here. Given a projective plane, fix four points in general position:  ,
,  ,
,  ,
,  , and let
, and let 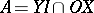 ,
,  and
and 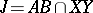 . For the points
. For the points 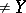 of
of 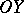 one chooses coordinates
one chooses coordinates 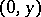 with
with 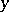 running over a set
running over a set 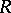 and
and 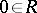 , assigning
, assigning 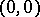 to
to 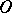 and
and 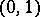 to
to  . The projection of
. The projection of 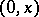 from
from 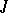 on
on 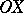 is given coordinates
is given coordinates 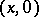 , and then
, and then 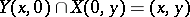 (see Fig.a1). The points on
(see Fig.a1). The points on 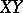 get one coordinate
get one coordinate  , with
, with  , or
, or 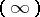 , where
, where 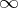 is an extra symbol
is an extra symbol 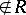 , and the lines are coordinatized by
, and the lines are coordinatized by 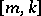 ,
, 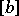 or
or 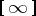 , as in Fig.a2.
, as in Fig.a2.
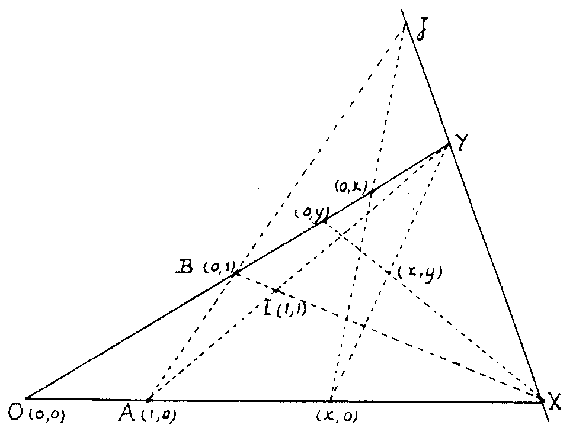
Figure: t092430a
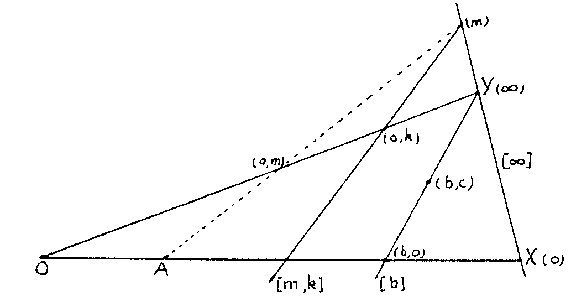
Figure: t092430b
The ternary operation  on
on 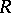 is defined by
is defined by 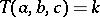 if and only if
if and only if 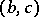 lies on
lies on 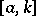 . The properties A)–E) for
. The properties A)–E) for 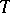 are then consequences of the axioms for a projective plane. Conversely, any ternary field coordinatizes a projective plane. It may happen that different ternary fields coordinatize the same plane, for a different choice of basis points
are then consequences of the axioms for a projective plane. Conversely, any ternary field coordinatizes a projective plane. It may happen that different ternary fields coordinatize the same plane, for a different choice of basis points  ,
,  ,
, 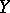 ,
, 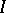 .
.
In case 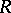 is finite, C) and D) are equivalent to D) and E); further, C) is then a consequence of D) and the existence of at most one
is finite, C) and D) are equivalent to D) and E); further, C) is then a consequence of D) and the existence of at most one  as in C).
as in C).
On a ternary field 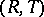 , addition is defined by
, addition is defined by 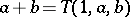 ; with this operation
; with this operation  is a loop with
is a loop with  as neutral element. Multiplication is defined by
as neutral element. Multiplication is defined by 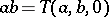 ; this makes
; this makes 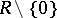 a loop with
a loop with 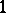 as neutral element.
as neutral element.  is said to be linear if
is said to be linear if 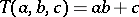 for all
for all  ,
, 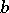 ,
,  . Linearity is equivalent to a very weak Desargues-type condition on triangles which are in perspective from the point
. Linearity is equivalent to a very weak Desargues-type condition on triangles which are in perspective from the point 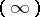 (cf. Configuration, in particular Desarguesian configuration, and also Desargues assumption). Other algebraic properties of
(cf. Configuration, in particular Desarguesian configuration, and also Desargues assumption). Other algebraic properties of 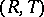 , such as associativity of addition or multiplication and left or right distributivity, can also be translated into certain Desargues-type conditions. In particular, a translation plane with
, such as associativity of addition or multiplication and left or right distributivity, can also be translated into certain Desargues-type conditions. In particular, a translation plane with  as translation line, i.e., a plane in which the group of
as translation line, i.e., a plane in which the group of 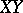 -translations is transitive on the points not on
-translations is transitive on the points not on 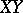 , is coordinatized by a (left) quasi-field, which is a linear ternary field with associative addition satisfying the left distributive law
, is coordinatized by a (left) quasi-field, which is a linear ternary field with associative addition satisfying the left distributive law 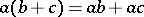 .
.
References
| [a1] | M. Hall, "Projective planes" Trans. Amer. Math. Soc. , 54 (1943) pp. 229–277 |
| [a2] | G. Pickert, "Projective Ebenen" , Springer (1975) |
| [a3] | D.R. Hughes, F.C. Piper, "Projective planes" , Springer (1973) |
Ternary field. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ternary_field&oldid=16138