Tangent line
to a curve
A straight line representing the limiting position of the secants. Let  be a point on a curve
be a point on a curve  (Fig. a). A second point
(Fig. a). A second point  is chosen on
is chosen on  and the straight line
and the straight line  is drawn. The point
is drawn. The point  is regarded as fixed, and
is regarded as fixed, and  approaches
approaches 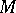 along the curve
along the curve  . If, as
. If, as  goes to
goes to  , the line
, the line  tends to a limiting line
tends to a limiting line  , then
, then  is called the tangent to
is called the tangent to  at
at  .
.

Figure: t092170a

Figure: t092170b
Not every continuous curve has a tangent, since  need not tend to a limiting position at all, or it may tend to two distinct limiting positions as
need not tend to a limiting position at all, or it may tend to two distinct limiting positions as  tends to
tends to 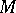 from different sides of
from different sides of  (Fig. b). If a curve in the plane with rectangular coordinates is defined by the equation
(Fig. b). If a curve in the plane with rectangular coordinates is defined by the equation 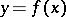 and
and  is differentiable at the point
is differentiable at the point  , then the slope of the tangent at
, then the slope of the tangent at 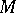 is equal to the value of the derivative
is equal to the value of the derivative 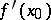 at
at  ; the equation of the tangent at this point has the form
; the equation of the tangent at this point has the form
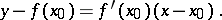 |
The equation of the tangent to a curve  in space is
in space is
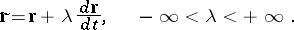 |
By a tangent to a surface  at a point
at a point 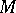 one means a straight line passing through
one means a straight line passing through  and lying in the tangent plane to
and lying in the tangent plane to  at
at  .
.
Comments
References
| [a1] | M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) (Translated from French) |
| [a2] | H.S.M. Coxeter, "Introduction to geometry" , Wiley (1961) |
| [a3] | H.W. Guggenheimer, "Differential geometry" , McGraw-Hill (1963) |
| [a4] | D. Hilbert, S.E. Cohn-Vossen, "Geometry and the imagination" , Chelsea (1952) (Translated from German) |
| [a5] | B. O'Neill, "Elementary differential geometry" , Acad. Press (1966) |
Tangent line. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tangent_line&oldid=14413