Symmetric space
A general name given to various types of spaces in differential geometry.
1) A manifold with an affine connection is called a locally symmetric affine space if the torsion tensor and the covariant derivative of the curvature tensor vanish identically.
2) A (pseudo-) Riemannian manifold is called a locally symmetric (pseudo-) Riemannian space if the covariant derivative of its curvature tensor with respect to the Levi-Civita connection vanishes identically.
3) A pseudo-Riemannian manifold (respectively, a manifold with an affine connection) 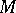 is called a globally symmetric pseudo-Riemannian (affine) space if one can assign to every point
is called a globally symmetric pseudo-Riemannian (affine) space if one can assign to every point 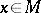 an isometry (affine transformation)
an isometry (affine transformation) 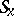 of
of 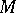 such that
such that 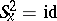 and
and  is an isolated fixed point of
is an isolated fixed point of 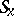 .
.
4) Let 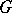 be a connected Lie group, let
be a connected Lie group, let 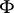 be an involutive automorphism
be an involutive automorphism 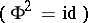 , let
, let 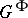 be the closed subgroup of all
be the closed subgroup of all 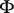 -fixed points, let
-fixed points, let 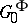 be the component of the identity in
be the component of the identity in 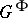 , and let
, and let 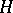 be a closed subgroup of
be a closed subgroup of 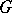 such that
such that
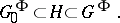 |
Then the homogeneous space  is called a symmetric homogeneous space.
is called a symmetric homogeneous space.
5) A symmetric space in the sense of Loos (a Loos symmetric space) is a manifold 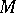 endowed with a multiplication
endowed with a multiplication
 |
satisfying the following four conditions:
a) 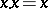 ;
;
b)  ;
;
c) 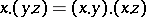 ;
;
d) every point 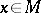 has a neighbourhood
has a neighbourhood 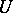 such that
such that 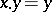 implies
implies  for all
for all 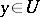 .
.
Any globally symmetric affine (pseudo-Riemannian) space is a locally symmetric affine (pseudo-Riemannian) space and a homogeneous symmetric space. Any homogeneous symmetric space is a globally symmetric affine space and a Loos symmetric space. Every connected Loos symmetric space is a homogeneous symmetric space.
Let 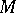 be a connected Loos symmetric space, and hence a homogeneous space:
be a connected Loos symmetric space, and hence a homogeneous space: 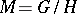 . Then
. Then  can be equipped with a torsion-free invariant affine connection with the following properties:
can be equipped with a torsion-free invariant affine connection with the following properties: 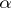 ) the covariant derivative of the curvature tensor vanishes;
) the covariant derivative of the curvature tensor vanishes; 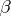 ) every geodesic
) every geodesic 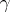 is a trajectory of some one-parameter subgroup
is a trajectory of some one-parameter subgroup 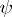 of
of 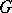 , and parallel translation of vectors along
, and parallel translation of vectors along 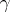 coincides with their translation by means of
coincides with their translation by means of  ; and
; and 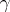 ) the geodesics are closed under multiplication (they are called one-dimensional subspaces). Similarly one can introduce the concept of an arbitrary subspace of
) the geodesics are closed under multiplication (they are called one-dimensional subspaces). Similarly one can introduce the concept of an arbitrary subspace of 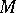 , namely, a manifold
, namely, a manifold 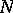 of
of 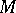 which is closed under multiplication and which is a symmetric space under the induced multiplication. A closed subset
which is closed under multiplication and which is a symmetric space under the induced multiplication. A closed subset 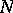 of
of 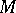 which is stable under multiplication is a subspace. The analogue of the Lie algebra for a symmetric space
which is stable under multiplication is a subspace. The analogue of the Lie algebra for a symmetric space 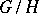 is defined as follows. Let
is defined as follows. Let 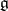 and
and  be the Lie algebras of the groups
be the Lie algebras of the groups  and
and  , respectively, and let
, respectively, and let 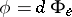 (the differential at the unit), where
(the differential at the unit), where 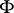 is the involutive automorphism defining the symmetric homogeneous space
is the involutive automorphism defining the symmetric homogeneous space 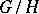 . The eigenvectors of the space endomorphism
. The eigenvectors of the space endomorphism 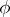 corresponding to the eigenvalue
corresponding to the eigenvalue 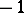 form a subspace
form a subspace  such that
such that 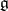 is the direct sum of the subspaces
is the direct sum of the subspaces 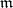 and
and 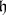 , and
, and  can be identified with the tangent space of
can be identified with the tangent space of 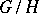 at the point
at the point 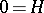 . If one defines a trilinear composition on the vector space
. If one defines a trilinear composition on the vector space 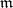 by
by
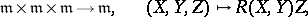 |
where  is the curvature tensor, then
is the curvature tensor, then 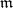 becomes a Lie ternary system. If
becomes a Lie ternary system. If 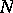 is a subspace of
is a subspace of 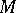 passing through the point 0, then the tangent space of
passing through the point 0, then the tangent space of  at 0 is a subsystem of
at 0 is a subsystem of 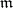 and conversely.
and conversely.
If 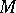 is a Loos symmetric space, then so is the product
is a Loos symmetric space, then so is the product 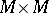 . Let
. Let 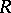 be a subspace of
be a subspace of 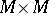 defining an equivalence relation on
defining an equivalence relation on 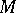 . Then
. Then 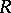 is called a congruence. This concept is used in the construction of a theory of coverings for symmetric spaces. Two points
is called a congruence. This concept is used in the construction of a theory of coverings for symmetric spaces. Two points 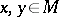 are said to commute if
are said to commute if
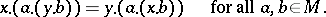 |
The centre  of
of 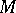 with respect to a point
with respect to a point 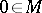 is defined to be the set of all points of
is defined to be the set of all points of 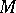 which commute with 0.
which commute with 0. 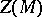 is a closed subspace of
is a closed subspace of 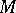 which can be equipped with an Abelian group structure. Let
which can be equipped with an Abelian group structure. Let 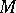 be a simply-connected symmetric space. Then the search for symmetric spaces for which
be a simply-connected symmetric space. Then the search for symmetric spaces for which 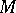 is a covering space reduces to the classification of discrete subgroups of
is a covering space reduces to the classification of discrete subgroups of 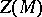 .
.
In the theory of symmetric spaces, considerable attention is devoted to classification problems (see ). Let 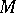 be a locally symmetric Riemannian space. Then
be a locally symmetric Riemannian space. Then 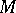 is called reducible if, in some coordinate system, its fundamental quadratic form can be written as
is called reducible if, in some coordinate system, its fundamental quadratic form can be written as
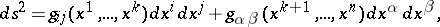 |
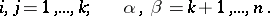 |
Otherwise the space is called irreducible. E. Cartan has shown that the study of all irreducible locally symmetric Riemannian spaces reduces to the classification of involutive automorphisms of real compact Lie algebras, which he accomplished. At the same time he solved the local classification problem for symmetric homogeneous spaces whose fundamental groups are simple and compact. A classification of symmetric homogeneous spaces with simple non-compact fundamental groups has been obtained (see , [3], [5]).
References
| [1] | P.A. Shirokov, "Selected works on geometry" , Kazan' (1966) (In Russian) |
| [2a] | E. Cartan, "Sur une classe rémarkable d'espaces de Riemann" Bull. Soc. Math. France , 54 (1926) pp. 214–264 |
| [2b] | E. Cartan, "Sur une classe rémarkable d'espaces de Riemann" Bull. Soc. Math. France , 55 (1927) pp. 114–134 |
| [3] | M. Berger, "Les espaces symmétriques noncompacts" Ann. Sci. École Norm. Sup. , 74 (1957) pp. 85–177 |
| [4] | O. Loos, "Symmetric spaces" , 1–2 , Benjamin (1969) |
| [5] | S. Helgason, "Differential geometry, Lie groups, and symmetric spaces" , Acad. Press (1978) |
Comments
Let 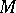 be a globally symmetric Riemannian space,
be a globally symmetric Riemannian space, 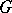 the connected component of the group of isometries of
the connected component of the group of isometries of 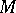 and
and 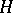 the isotropy subgroup of
the isotropy subgroup of 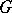 of some point of
of some point of 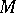 . Then definitions can be given for
. Then definitions can be given for 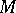 being of compact, non-compact or Euclidean type in terms of the corresponding pair of Lie algebras
being of compact, non-compact or Euclidean type in terms of the corresponding pair of Lie algebras  . In particular, if
. In particular, if 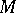 is of the non-compact type, then
is of the non-compact type, then 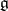 has a Cartan decomposition
has a Cartan decomposition 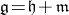 , see [5].
, see [5].
References
| [a1] | A.L. Besse, "Einstein manifolds" , Springer (1987) |
| [a2] | B.A. [B.A. Rozenfel'd] Rosenfel'd, "A history of non-euclidean geometry" , Springer (1988) (Translated from Russian) |
Symmetric space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Symmetric_space&oldid=11484