Symmetric design
symmetric block design
A  -design (or balanced incomplete block design, cf. BIBD) which satisfies Fisher's inequality
-design (or balanced incomplete block design, cf. BIBD) which satisfies Fisher's inequality 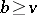 (cf. also Block design) with equality. More precisely, a symmetric
(cf. also Block design) with equality. More precisely, a symmetric  -design is an incidence structure consisting of
-design is an incidence structure consisting of  points and
points and  blocks (cf. also Block design) of size
blocks (cf. also Block design) of size 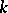 (that is,
(that is, 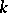 -subsets of the point set), such that any two distinct points are on precisely
-subsets of the point set), such that any two distinct points are on precisely  common blocks. It can be shown that then also any two distinct blocks intersect in precisely
common blocks. It can be shown that then also any two distinct blocks intersect in precisely 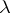 points, see [a1], § II.3.
points, see [a1], § II.3.
The outstanding problem in this area (1998) is to characterize the possible parameter triples  . A simple counting argument gives the equation
. A simple counting argument gives the equation  , which provides a trivial necessary existence condition. A non-trivial restriction is the Bruck–Ryser–Chowla theorem, see Block design. This condition is not sufficient, as the non-existence of a symmetric
, which provides a trivial necessary existence condition. A non-trivial restriction is the Bruck–Ryser–Chowla theorem, see Block design. This condition is not sufficient, as the non-existence of a symmetric 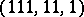 -design, i.e. a projective plane of order
-design, i.e. a projective plane of order 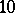 , shows; see [a5].
, shows; see [a5].
There are more than 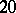 known infinite series of symmetric designs (as of 1998). The most classical examples are the symmetric designs
known infinite series of symmetric designs (as of 1998). The most classical examples are the symmetric designs 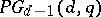 formed by the points and hyperplanes of the
formed by the points and hyperplanes of the  -dimensional finite projective space
-dimensional finite projective space 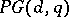 over the Galois field of order
over the Galois field of order 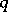 (so
(so  is a prime power here) and the Hadamard
is a prime power here) and the Hadamard  -designs (or Hadamard configurations) with parameters of the form
-designs (or Hadamard configurations) with parameters of the form 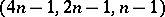 ; such a design is equivalent to a Hadamard matrix of order
; such a design is equivalent to a Hadamard matrix of order 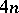 , which is conjectured to exist for all values of
, which is conjectured to exist for all values of  . Similarly, a symmetric design with parameters of the form
. Similarly, a symmetric design with parameters of the form
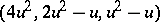 | (a1) |
is equivalent to a regular Hadamard matrix of order 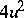 , that is, a Hadamard matrix with constant row and column sums; these are conjectured to exist for all values of
, that is, a Hadamard matrix with constant row and column sums; these are conjectured to exist for all values of  . Many examples are known, e.g. whenever
. Many examples are known, e.g. whenever  is the product of a perfect square with an arbitrary number of the form
is the product of a perfect square with an arbitrary number of the form 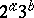 . An important recent (1998) construction method for symmetric designs which combines Abelian difference sets (cf. Abelian difference set; Difference set; Difference set (update)) with so-called balanced generalized weighing matrices yields seven infinite families; this is due to Y.J. Ionin [a3]. See [a1], [a2] for lists of the known (1998) infinite series, tables of small symmetric designs and some constructions.
. An important recent (1998) construction method for symmetric designs which combines Abelian difference sets (cf. Abelian difference set; Difference set; Difference set (update)) with so-called balanced generalized weighing matrices yields seven infinite families; this is due to Y.J. Ionin [a3]. See [a1], [a2] for lists of the known (1998) infinite series, tables of small symmetric designs and some constructions.
In general, a symmetric design cannot be characterized just by its parameters. For instance, the number of non-isomorphic designs with the same parameters as 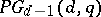 grows exponentially with a growth rate of at least
grows exponentially with a growth rate of at least 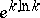 , where
, where 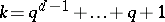 . Hence it is desirable to characterize the designs
. Hence it is desirable to characterize the designs  as well as other particularly interesting designs. For instance, the Dembowski–Wagner theorem states that a symmetric design
as well as other particularly interesting designs. For instance, the Dembowski–Wagner theorem states that a symmetric design 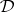 with
with  in which every line (that is, the intersection of all blocks through two given points) meets every block is isomorphic to some
in which every line (that is, the intersection of all blocks through two given points) meets every block is isomorphic to some 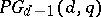 ; the same conclusion holds if
; the same conclusion holds if 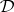 admits an automorphism group which is transitive on ordered triples of non-collinear points. See [a1], § XII.2, for proofs and further characterizations.
admits an automorphism group which is transitive on ordered triples of non-collinear points. See [a1], § XII.2, for proofs and further characterizations.
Symmetric designs with a "nice" automorphism group are of particular interest. The orbit theorem states that any automorphism group 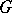 of a symmetric design
of a symmetric design 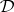 has equally many orbits on points and blocks (cf. also Orbit). In particular,
has equally many orbits on points and blocks (cf. also Orbit). In particular, 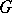 is transitive (cf. Transitive group) on points if and only if it is transitive on blocks. In this case, the permutation rank of
is transitive (cf. Transitive group) on points if and only if it is transitive on blocks. In this case, the permutation rank of 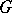 on points agrees with that on blocks (cf. also Rank of a group). In the special case where
on points agrees with that on blocks (cf. also Rank of a group). In the special case where 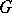 has rank
has rank  (and thus is doubly transitive on both points and blocks), a complete classification was given by W.M. Kantor [a4]: There are two infinite series, namely the classical designs
(and thus is doubly transitive on both points and blocks), a complete classification was given by W.M. Kantor [a4]: There are two infinite series, namely the classical designs 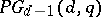 and another series which has parameters of the form (a1), where
and another series which has parameters of the form (a1), where  is a power of
is a power of  ; the latter examples all admit a symplectic group as automorphism group. In addition, there are two sporadic examples, namely the Hadamard
; the latter examples all admit a symplectic group as automorphism group. In addition, there are two sporadic examples, namely the Hadamard  -design on
-design on 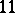 points and a
points and a  -design which admits the Higman–Sims group, one of the
-design which admits the Higman–Sims group, one of the 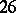 sporadic simple groups (cf. also Sporadic simple group). On the other end of the spectrum, there is the case of permutation rank
sporadic simple groups (cf. also Sporadic simple group). On the other end of the spectrum, there is the case of permutation rank  , i.e.
, i.e. 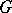 is regular (cf. Permutation group) on both points and blocks; such a group is called a Singer group of
is regular (cf. Permutation group) on both points and blocks; such a group is called a Singer group of 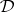 , generalizing the notion of a Singer cycle. In this case,
, generalizing the notion of a Singer cycle. In this case, 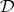 is equivalent to a
is equivalent to a 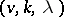 -difference set
-difference set 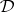 in
in  (cf. also Difference set; Abelian difference set): Up to isomorphism,
(cf. also Difference set; Abelian difference set): Up to isomorphism, 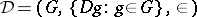 . A complete classification is yet (1998) out of reach, even in the Abelian case. For instance, it is widely conjectured that a projective plane of finite order
. A complete classification is yet (1998) out of reach, even in the Abelian case. For instance, it is widely conjectured that a projective plane of finite order  admitting a Singer group must be Desarguesian (cf. also Desargues geometry), at least in the cyclic case; but only for a few values of
admitting a Singer group must be Desarguesian (cf. also Desargues geometry), at least in the cyclic case; but only for a few values of 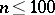 , this is actually proven. However, there is ample evidence for the validity of the weaker prime power conjecture, which asserts that the order
, this is actually proven. However, there is ample evidence for the validity of the weaker prime power conjecture, which asserts that the order  of a finite projective plane admitting an Abelian Singer group must be a prime power; this is now known to hold whenever
of a finite projective plane admitting an Abelian Singer group must be a prime power; this is now known to hold whenever 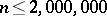 . See [a1], § VI.7, where this topic is studied in the language of planar difference sets.
. See [a1], § VI.7, where this topic is studied in the language of planar difference sets.
References
| [a1] | T. Beth, D. Jungnickel, H. Lenz, "Design theory" , Cambridge Univ. Press (1999) (Edition: Second) |
| [a2] | C.J. Colbourn, J.H. Dinitz, "The CRC Handbook of combinatorial designs" , CRC (1996) |
| [a3] | Y.J. Ionin, "Building symmetric designs with building sets" Designs, Codes and Cryptography , 17 (1999) pp. 159–175 |
| [a4] | W.M. Kantor, " -transitive symmetric designs" Graphs Combin. , 1 (1985) pp. 165–166 -transitive symmetric designs" Graphs Combin. , 1 (1985) pp. 165–166 |
| [a5] | C.W.H. Lam, L.H. Thiel, S. Swiercz, "The non-existence of finite projective planes of order 10" Canad. J. Math. , 41 (1989) pp. 1117–1123 |
Symmetric design. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Symmetric_design&oldid=12425