Suspension

of a topological space (CW-complex)

The space (CW-complex)

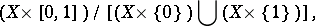where is the unit interval and the slant line denotes the operation of identifying a subspace with one point. The suspension of a pointed space is defined to be the pointed space

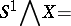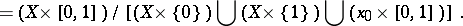This is also known as a reduced or contracted suspension. A suspension is denoted by (or sometimes ). The correspondence defines a functor from the category of topological (pointed) spaces into itself.

Since the suspension operation is a functor, one can define a homomorphism 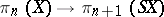, which is also called the suspension. This homomorphism is identical with the composite of the homomorphism induced by the imbedding and the Hurewicz isomorphism 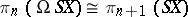, where is the operation of forming loop spaces (cf. Loop space). For any homology theory 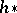(cohomology theory ) one has an isomorphism

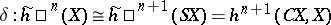that coincides with the connecting homomorphism of the exact sequence of the pair 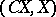, where is the cone over . The image of a class under this isomorphism is known as the suspension of and is denoted by (or ).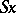

The suspension of a cohomology operation is defined to be the cohomology operation whose action on coincides with , and whose action on coincides with that of .

Comments

The suspension functor and the loop space functor on the category of pointed spaces are adjoint:

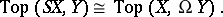The bijection above associates to the mapping 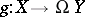which associates the loop to 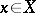. This adjointness is compatible with the homology and thus also defines an adjunction for the category of pointed topological spaces and homotopy classes of mappings.

References

[a1]	R.M. Switzer, "Algebraic topology - homotopy and homology" , Springer (1975) pp. Chapt. 2