Surface
One of the basic concepts in geometry. The definitions of a surface in various fields of geometry differ substantially.
In elementary geometry, one considers planes, multi-faced surfaces, as well as certain curved surfaces (for example, spheres). Each curved surface is defined in a special way, very often as a set of points or lines. The general concept of surface is only explained, not defined, in elementary geometry: One says that a surface is the boundary of a body, or the trace of a moving line, etc.
In analytic and algebraic geometry, a surface is considered as a set of points the coordinates of which satisfy equations of a particular form (see, for example, Surface of the second order; Algebraic surface).
In three-dimensional Euclidean space 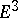 , a surface is defined by means of the concept of a surface patch — a homeomorphic image of a square in
, a surface is defined by means of the concept of a surface patch — a homeomorphic image of a square in 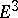 . A surface is understood to be a connected set which is the union of surface patches (for example, a sphere is the union of two hemispheres, which are surface patches).
. A surface is understood to be a connected set which is the union of surface patches (for example, a sphere is the union of two hemispheres, which are surface patches).
Usually, a surface is specified in 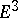 by a vector function
by a vector function
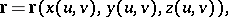 |
where  , while
, while
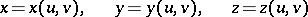 |
are functions of parameters  and
and  that satisfy certain regularity conditions, for example, the condition
that satisfy certain regularity conditions, for example, the condition
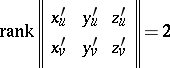 |
(see also Differential geometry; Theory of surfaces; Riemannian geometry).
From the point of view of topology, a surface is a two-dimensional manifold.
Comments
References
| [a1] | J.J. Stoker, "Differential geometry" , Wiley (Interscience) (1969) |
| [a2] | J.A. Thorpe, "Elementary topics in differential geometry" , Springer (1979) |
Surface. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Surface&oldid=11661