Subseries convergence
If  is a Hausdorff Abelian topological group, a series
is a Hausdorff Abelian topological group, a series  in
in  is
is  -subseries convergent (respectively, unconditionally convergent) if for each subsequence
-subseries convergent (respectively, unconditionally convergent) if for each subsequence  (respectively, each permutation
(respectively, each permutation  ) of
) of  , the subseries
, the subseries  (respectively, the rearrangement
(respectively, the rearrangement 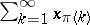 ) is
) is  -convergent in
-convergent in  . In one of the early papers in the history of functional analysis, W. Orlicz showed that if
. In one of the early papers in the history of functional analysis, W. Orlicz showed that if  is a weakly sequentially complete Banach space, then a series in
is a weakly sequentially complete Banach space, then a series in 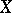 is weakly unconditionally convergent if and only if the series is norm unconditionally convergent [a5]. Later, he noted that if "unconditional convergence" is replaced by "subseries convergence" , the proof showed that the weak sequential completeness assumption could be dropped. That is, a series in a Banach space is weakly subseries convergent if and only if the series is norm subseries convergent; this result was announced in [a1], but no proof was given. In treating some problems in vector-valued measure and integration theory, B.J. Pettis needed to use this result but noted that no proof was supplied and then proceeded to give a proof ([a6]; the proof is very similar to that of Orlicz). The result subsequently came to be known as the Orlicz–Pettis theorem (see [a3] for a historical discussion).
is weakly unconditionally convergent if and only if the series is norm unconditionally convergent [a5]. Later, he noted that if "unconditional convergence" is replaced by "subseries convergence" , the proof showed that the weak sequential completeness assumption could be dropped. That is, a series in a Banach space is weakly subseries convergent if and only if the series is norm subseries convergent; this result was announced in [a1], but no proof was given. In treating some problems in vector-valued measure and integration theory, B.J. Pettis needed to use this result but noted that no proof was supplied and then proceeded to give a proof ([a6]; the proof is very similar to that of Orlicz). The result subsequently came to be known as the Orlicz–Pettis theorem (see [a3] for a historical discussion).
Since the Orlicz–Pettis theorem has many applications, particularly to the area of vector-valued measure and integration theory, there have been attempts to generalize the theorem in several directions. For example, A. Grothendieck remarked that the result held for locally convex spaces and a proof was supplied by C.W. McArthur. Recent (1998) results have attempted to push subseries convergence to topologies on the space which are stronger than the original topology (for references to these results, see the historical survey of [a4]).
In the case of a Banach space  , attempts have been made to replace the weak topology of
, attempts have been made to replace the weak topology of  by a weaker topology,
by a weaker topology,  , generated by a subspace
, generated by a subspace 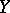 of the dual space of
of the dual space of  which separates the points of
which separates the points of  . Perhaps the best result in this direction is the Diestel–Faires theorem, which states that if
. Perhaps the best result in this direction is the Diestel–Faires theorem, which states that if 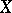 contains no subspace isomorphic to
contains no subspace isomorphic to 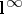 , then a series in
, then a series in  is
is 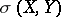 subseries convergent if and only if the series is norm subseries convergent. If
subseries convergent if and only if the series is norm subseries convergent. If 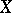 is the dual of a Banach space
is the dual of a Banach space  and
and 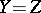 , then the converse also holds (see [a2], for references and further results).
, then the converse also holds (see [a2], for references and further results).
J. Stiles gave what is probably the first extension of the Orlicz–Pettis theorem to non-locally convex spaces; namely, he established a version of the theorem for a complete metric linear space with a Schauder basis. This leads to a very general form of the theorem by N. Kalton in the context of Abelian topological groups (see [a4] for references on these and further results).
References
| [a1] | S. Banach, "Théoriè des opérations linéaires" , Monogr. Mat. Warsaw (1932) |
| [a2] | J. Diestel, J. Uhl, "Vector measures" , Surveys , 15 , Amer. Math. Soc. (1977) |
| [a3] | W. Filter, I. Labuda, "Essays on the Orlicz–Pettis theorem I" Real Anal. Exch. , 16 (1990/91) pp. 393–403 |
| [a4] | N. Kalton, "The Orlicz–Pettis theorem" Contemp. Math. , 2 (1980) |
| [a5] | W. Orlicz, "Beiträge zur Theorie der Orthogonalent wicklungen II" Studia Math. , 1 (1929) pp. 241–255 |
| [a6] | B.J. Pettis, "On integration in vector spaces" Trans. Amer. Math. Soc. , 44 (1938) pp. 277–304 |
Subseries convergence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Subseries_convergence&oldid=13868