Strong Stieltjes moment problem
The strong Stieltjes moment problem for a given sequence 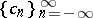 of real numbers is concerned with finding real-valued, bounded, monotone non-decreasing functions
of real numbers is concerned with finding real-valued, bounded, monotone non-decreasing functions 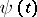 with infinitely many points of increase for
with infinitely many points of increase for 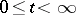 such that
such that
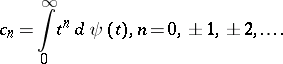 | (a1) |
This problem, which generalizes the classical Stieltjes moment problem (where the given sequence is 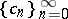 ; cf. also Krein condition), was first studied by W.B. Jones, W.J. Thron and H. Waadeland [a1].
; cf. also Krein condition), was first studied by W.B. Jones, W.J. Thron and H. Waadeland [a1].
Let 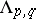 be the complex linear space spanned by the set of functions
be the complex linear space spanned by the set of functions  with
with 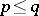 , and define
, and define 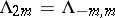 and
and 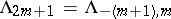 for
for 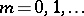 , and
, and 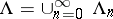 . An element of
. An element of 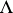 is called a Laurent polynomial. For a given sequence
is called a Laurent polynomial. For a given sequence 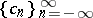 , a necessary and sufficient condition for the strong Stieltjes moment problem to be solvable is that the linear operator
, a necessary and sufficient condition for the strong Stieltjes moment problem to be solvable is that the linear operator 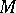 defined on the base elements
defined on the base elements 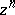 of
of 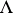 by
by
 | (a2) |
is positive on 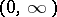 , i.e. for any
, i.e. for any 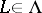 such that
such that 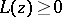 for
for 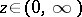 and
and 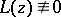 , then
, then 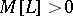 . An equivalent condition is that if
. An equivalent condition is that if
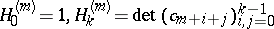 | (a3) |
for 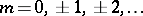 ,
, 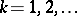 , are the Hankel determinants associated with
, are the Hankel determinants associated with 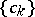 (cf. also Hankel matrix), then
(cf. also Hankel matrix), then
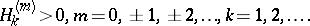 |
Orthogonal Laurent polynomials 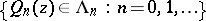 may be defined with respect to the inner product
may be defined with respect to the inner product 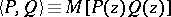 and are given by:
and are given by:
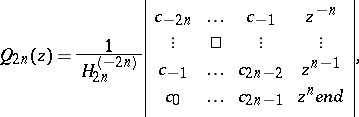 | (a4) |
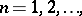 |
and
 | (a5) |
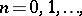 |
and 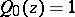 . Corresponding associated orthogonal Laurent polynomials
. Corresponding associated orthogonal Laurent polynomials 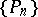 are defined by
are defined by
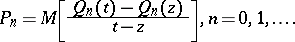 | (a6) |
The rational functions 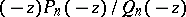 are the convergents of the positive T-fraction [a3],
are the convergents of the positive T-fraction [a3],
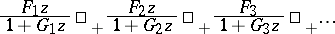 | (a7) |
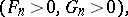 |
where
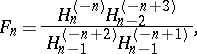 |
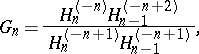 |
which corresponds to the formal pair of power series,
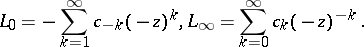 | (a8) |
The T-fraction is equivalent to the continued fraction
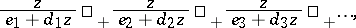 | (a9) |
where
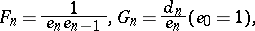 | (a10) |
 |
The following result may then be proved [a1]: The solution of the strong Stieltjes moment problem (a1) is unique if and only if at least one of the series 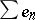 ,
, 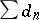 diverges, and then
diverges, and then
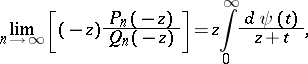 | (a11) |
where 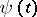 is this unique solution.The convergence is uniform on every compact subset of
is this unique solution.The convergence is uniform on every compact subset of 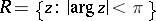 .
.
The strong Stieltjes moment problem is said to be determinate when it has a unique solution and indeterminate otherwise. A detailed discussion of the latter case has been given in [a4].
A classic example of a strong Stieltjes moment problem is the log-normal distribution,
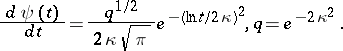 |
(Cf. also Normal distribution.) The corresponding sequence of moments is 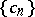 , where
, where
 |
and the strong Stieltjes moment problem in this case is indeterminate [a5]. The moments corresponding to the log-normal distribution are related to a subclass of strong Stieltjes moment problems where
 |
This subclass has been called strong symmetric Stieltjes moment problems by A.K. Common and J. McCabe, who studied properties of the related continued fractions [a6]. Other subclasses have been investigated in [a7].
Cf. also Moment problem.
References
| [a1] | W.B. Jones, O. Njåstad, W.J. Thron, "A strong Stieltjes moment problem" Trans. Amer. Math. Soc. , 261 (1980) pp. 503–528 |
| [a2] | W.B. Jones, O. Njåstad, W.J. Thron, "Continued fractions and strong Hamburger moment problems" Proc. London Math. Soc. , 47 (1983) pp. 105–123 |
| [a3] | W.B. Jones, W.J. Thron, "Continued fractions: Analytic theory and applications" , Encycl. Math. Appl. , 11 , Addison-Wesley (1980) |
| [a4] | O. Njåstad, "Solutions of the strong Stieltjes moment problem" Meth. Appl. Anal. , 2 (1995) pp. 320–347 |
| [a5] | S.C. Cooper, W.B. Jones, W.J. Thron, "Orthogonal Laurent polynomials and continued fractions associated with log-normal distributions" J. Comput. Appl. Math. , 32 (1990) pp. 39–46 |
| [a6] | A.K. Common, J. McCabe, "The symmetric strong moment problem" J. Comput. Appl. Math. , 67 (1996) pp. 327–341 |
| [a7] | A. Sri Ranga, E.X.L. de Andrade, J. McCabe, "Some consequences of symmetry in strong distributions" J. Math. Anal. Appl. , 193 (1995) pp. 158–168 |
Strong Stieltjes moment problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Strong_Stieltjes_moment_problem&oldid=14838