Stochastic processes, prediction of
extrapolation of stochastic processes
The problem of estimating the values of a stochastic process 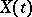 in the future
in the future  from its observed values up to the current moment of time
from its observed values up to the current moment of time  . Usually one has in mind the extrapolation estimator
. Usually one has in mind the extrapolation estimator  ,
,  , for which the mean-square error
, for which the mean-square error  is minimal over all estimators based on the past values of the process up to the moment
is minimal over all estimators based on the past values of the process up to the moment  (the prediction is called linear if one restricts consideration to linear estimators).
(the prediction is called linear if one restricts consideration to linear estimators).
One of the problems posed and solved was that of linear prediction of a stationary sequence. This problem is analogous to the following: In the space  of square-integrable functions on the interval
of square-integrable functions on the interval  one has to find the projection of the function
one has to find the projection of the function 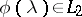 onto the subspace generated by the functions
onto the subspace generated by the functions  ,
,  . This problem has been greatly generalized in the theory of stationary stochastic processes (cf. Stationary stochastic process). One application is the problem of predicting stochastic processes arising from the system
. This problem has been greatly generalized in the theory of stationary stochastic processes (cf. Stationary stochastic process). One application is the problem of predicting stochastic processes arising from the system
 |
where 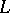 is a linear differential operator of order
is a linear differential operator of order  and
and 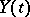 ,
,  , is a white noise process. The optimal prediction
, is a white noise process. The optimal prediction 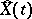 ,
, 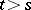 , given the values of
, given the values of 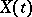 at the times
at the times 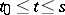 and the initial values
and the initial values  ,
, 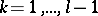 , independent of white noise, is obtained by solving the corresponding equation
, independent of white noise, is obtained by solving the corresponding equation
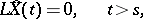 |
with initial conditions
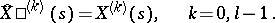 |
For systems of stochastic differential equations, the problem of predicting some components given the values of other observed components reduces to the extrapolation of the corresponding stochastic equations.
For references see Stochastic processes, interpolation of.
Comments
Study of the linear prediction problem was initiated by A.N. Kolmogorov in Russia [a7], [a8], and in the West by N. Wiener [a6], who also, with P. Masani, treated the multivariate case [a11], [a12]. They considered prediction based on the entire past; prediction based on a finite segment of the past is more subtle, see [a9], [a10]. Linear prediction for non-stationary processes is covered in [a13]. The linear theory may also be found in [a2]. The approach of R.E. Kalman [a3], [a4] has produced practically usable prediction algorithms, based on the Kalman filter and on state space realizations of the underlying processes. A generalization of the prediction problem to diffusion processes is presented in [a5]. For applications of prediction algorithms in the applied sciences see [a1].
References
| [a1] | G.E.P. Box, G.M. Jenkins, "Time series analysis. Forecasting and control" , Holden-Day (1976) |
| [a2] | E.J. Hannan, "Multiple time series" , Wiley (1970) |
| [a3] | R.E. Kalman, "A new approach to linear filtering and prediction problems" J. Basic Eng., Trans. ASME, Series D , 82 : 1 (March 1960) pp. 35–45 |
| [a4] | R.E. Kalman, R.S. Bucy, "New results in linear filtering and prediction theory" J. Basic Eng., Trans. ASME, Series D , 83 (1961) pp. 95–108 |
| [a5] | E. Pardoux, "Equations du filtrage nonlinéaire, de la prédiction et du lissage" Stochastics , 6 (1982) pp. 193–231 |
| [a6] | N. Wiener, "Extrapolation, interpolation, and smoothing of stationary time series: with engineering applications" , M.I.T. (1949) |
| [a7] | A.N. Kolmogorov, "Stationary sequences in Hilbert space" Byull. Moskov. Gos. Univ. Sect. A , 2 : 6 (1941) pp. 1–40 (In Russian) |
| [a8] | A.N. Kolmogorov, "Interpolation und Extrapolation von stationären zufalligen Folgen" Izv. Akad. Nauk. SSSR , 5 (1941) pp. 3–14 |
| [a9] | M.G. Krein, "On a fundamental approximation problem in the theory of extrapolation and filtration of stationary random processes" Amer. Math. Soc. Sel. Transl. Math. Statist. , 4 (1964) pp. 127–131 Dokl. Akad. Nauk. SSSR , 94 (1954) pp. 13–16 |
| [a10] | H. Dym, H.P. McKean, "Gaussian processes, function theory and the inverse spectral problem" , Acad. Press (1976) |
| [a11] | N. Wiener, P. Masani, "The prediction theory of multivariate stochastic processes I" Acta Math. , 98 (1957) pp. 111–150 |
| [a12] | N. Wiener, P. Masani, "The prediction theory of multivariate stochastic processes II" Acta Math. , 99 (1958) pp. 93–137 |
| [a13] | J. Rissanen, L. Barbosa, "A factorization problem and the problem of predicting non-stationary vector-valued random processes" Z. Wahrscheinlichkeitstheorie verw. Geb. , 12 (1969) pp. 255–266 |
Stochastic processes, prediction of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stochastic_processes,_prediction_of&oldid=15885