Stochastic processes, interpolation of
The problem of estimating the values of a stochastic process  on some interval
on some interval  using its observed values outside this interval. Usually one has in mind the interpolation estimator
using its observed values outside this interval. Usually one has in mind the interpolation estimator  for which the mean-square error of interpolation is minimal compared to all other estimators:
for which the mean-square error of interpolation is minimal compared to all other estimators:
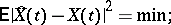 |
the interpolation is called linear if one restricts attention to linear estimators. One of the first problems posed and solved was that of linear interpolation of the value  of a stationary sequence. This problem is analogous to the following one: In the space
of a stationary sequence. This problem is analogous to the following one: In the space  of square-integrable functions on the interval
of square-integrable functions on the interval  , one must find the projection of
, one must find the projection of  onto the subspace generated by the functions
onto the subspace generated by the functions  ,
, 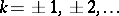 . This problem has been greatly generalized in the theory of stationary stochastic processes (cf. Stationary stochastic process; [1], [2]). One application is the problem of interpolation of the stochastic process arising from the system
. This problem has been greatly generalized in the theory of stationary stochastic processes (cf. Stationary stochastic process; [1], [2]). One application is the problem of interpolation of the stochastic process arising from the system
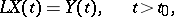 |
where 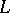 is a linear differential operator of order
is a linear differential operator of order 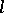 , and
, and 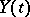 ,
, 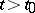 , is a white noise process. For given initial values
, is a white noise process. For given initial values 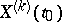 ,
, 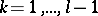 , independent of the white noise, the optimal interpolation estimator
, independent of the white noise, the optimal interpolation estimator 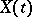 ,
, 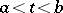 , is the solution of the corresponding boundary value problem
, is the solution of the corresponding boundary value problem
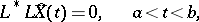 |
where 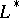 denotes the formal adjoint operator,
denotes the formal adjoint operator,
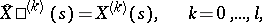 |
with boundary conditions at the boundary points 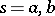 . For systems of stochastic differential equations the problem of interpolation of some components given the values of other observed components reduces to similar interpolation equations. (See [3].)
. For systems of stochastic differential equations the problem of interpolation of some components given the values of other observed components reduces to similar interpolation equations. (See [3].)
References
| [1] | A.N. Kolmogorov, "Stationary sequences in Hilbert space" Byull. Moskov. Gos. Univ. Sekt. A , 2 : 6 (1941) pp. 1–40 (In Russian) |
| [2] | Yu.A. Rozanov, "Stationary stochastic processes" , Holden-Day (1967) (Translated from Russian) |
| [3] | R.S. Liptser, A.N. Shiryaev, "Statistics of stochastic processes" , 1–2 , Springer (1977–1978) (Translated from Russian) |
Comments
The interpolation problem is usually defined as the estimation of an unobserved stochastic process on some time interval given a related stochastic process that is observed outside this time interval. One distinguishes two special cases: 1) linear least-squares interpolation, in which the estimator is constrained to be linear and minimizes a least-squares criterion, see [a1], [a3]; and 2) interpolation in which the conditional distribution of the estimator given the observations is determined, see [a2].
For the Western literature on interpolation see [a5], Sect. 5.3 and [a1], Sect. 4.13. Additional Russian references that have been translated are [a6]; [a7], Sect. 37. For recent developments using stochastic realization theory see [a3], [a4]. Results for the interpolation problem may also be deduced from those for the smoothing problem [a2].
References
| [a1] | H. Dym, H.P. McKean, "Gaussian processes, function theory, and the inverse spectral problem" , Acad. Press (1976) |
| [a2] | E. Pardoux, "Equations du filtrage nonlinéaire, de la prédiction et du lissage" Stochastics , 6 (1982) pp. 193–231 |
| [a3] | M. Pavon, "New results on the interpolation problem for continuous-time stationary increment processes" SIAM J. Control Optim. , 22 (1984) pp. 133–142 |
| [a4] | M. Pavon, "Optimal interpolation for linear stochastic systems" SIAM J. Control Optim. , 22 (1984) pp. 618–629 |
| [a5] | N. Wiener, "Extrapolation, interpolation, and smoothing of stationary time series: with engineering applications" , M.I.T. (1949) |
| [a6] | A.M. Yaglom, "Extrapolation, interpolation and filtration of stationary random processes with rational spectral density" Amer. Math. Soc. Sel. Transl. Math. Statist. , 4 (1963) pp. 345–387 Tr. Moskov. Mat. Obshch. , 4 (1955) pp. 333–374 |
| [a7] | A.M. Yaglom, "An introduction to the theory of stationary random functions" , Prentice-Hall (1962) (Translated from Russian) |
Stochastic processes, interpolation of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stochastic_processes,_interpolation_of&oldid=17488