Stochastic integration via the Fock space of white noise
Consider the probability space of (commutative) white noise 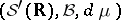 , where
, where  is the topological
is the topological 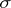 -algebra of
-algebra of 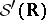 and
and 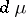 is the measure determined by
is the measure determined by
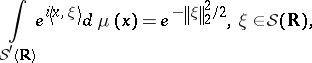 | (a1) |
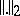 being the norm of
being the norm of 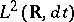 and
and 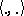 denoting the dual pairing.
denoting the dual pairing.  is unitary to the symmetric Fock space
is unitary to the symmetric Fock space
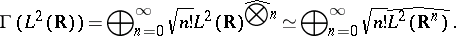 | (a2) |
One can identify the last two spaces and denotes the unitary mapping from 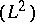 onto
onto 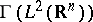 by
by 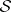 .
.
Informally, one is looking for a pair 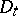 ,
, 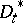 of operators acting on the Fock space which implement the canonical commutation relations (cf. also Commutation and anti-commutation relationships, representation of)
of operators acting on the Fock space which implement the canonical commutation relations (cf. also Commutation and anti-commutation relationships, representation of)
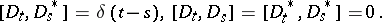 | (a3) |
Still informally, this can be achieved as follows. If 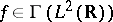 ,
, 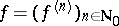 ,
, 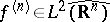 , set
, set
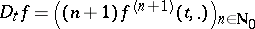 | (a4) |
and let 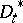 be the informal adjoint, i.e.
be the informal adjoint, i.e.
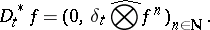 | (a5) |
This is made rigorous by introducing a suitable (complete) subspace 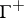 of
of  with dual
with dual 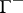 , so that one has a Gel'fand triple
, so that one has a Gel'fand triple 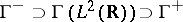 (cf. also Gel'fand representation) whose isomorphic pre-image gives the triple
(cf. also Gel'fand representation) whose isomorphic pre-image gives the triple 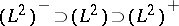 . For choices of
. For choices of  , see e.g. [a5], [a6], [a7], [a8], [a9], [a12]. Then
, see e.g. [a5], [a6], [a7], [a8], [a9], [a12]. Then 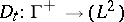 ,
, 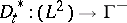 . Denote the corresponding operators on
. Denote the corresponding operators on 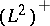 and
and 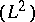 by
by  and
and 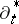 , respectively. It turns out that multiplication by white noise is well-defined as an operator from
, respectively. It turns out that multiplication by white noise is well-defined as an operator from 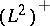 into
into 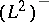 by
by 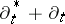 [a7], [a8], [a9]. In particular, Brownian motion may be defined as
[a7], [a8], [a9]. In particular, Brownian motion may be defined as
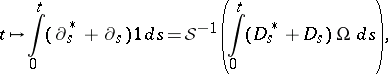 |
 being the Fock space vacuum
being the Fock space vacuum 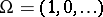 .
.
Consider a process 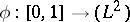 and assume for simplicity that this mapping is continuous. If one wishes to define the stochastic integral of
and assume for simplicity that this mapping is continuous. If one wishes to define the stochastic integral of 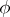 with respect to Brownian motion
with respect to Brownian motion 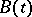 ,
, 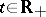 , then one may set for
, then one may set for 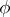 taking values in
taking values in  ,
,
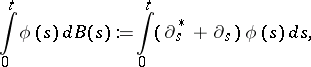 | (a6) |
following the heuristic idea that the "time derivative of Brownian motion is white noise" . However, for most of the processes 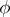 of interest (e.g. Brownian motion itself), one does not have
of interest (e.g. Brownian motion itself), one does not have 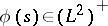 and therefore the second term on the right-hand side of (a6) would be ill-defined. Moreover, heuristic calculations show [a9], [a11] that one should replace the term
and therefore the second term on the right-hand side of (a6) would be ill-defined. Moreover, heuristic calculations show [a9], [a11] that one should replace the term 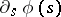 in (a6) by a proper version of
in (a6) by a proper version of
 |
in order to reproduce the standard Itô integral (cf. also Itô formula). This extension of the operator 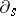 can be defined using a subspace of
can be defined using a subspace of 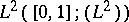 , constructed by means of the trace theorem of Sobolev spaces [a9], [a3]. So, put
, constructed by means of the trace theorem of Sobolev spaces [a9], [a3]. So, put
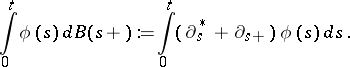 | (a7) |
It can be shown [a9] that for processes 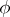 adapted to the filtration generated by Brownian motion,
adapted to the filtration generated by Brownian motion, 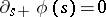 for all
for all 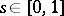 and that the resulting stochastic integral (a7) coincides with the Itô-integral of
and that the resulting stochastic integral (a7) coincides with the Itô-integral of 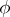 . Thus, (a7) is an extension of Itô's integral to anticipating processes. Clearly, also the first term on the right-hand side of (a7) alone is an extension of the Itô-integral to non-adapted processes and it is the white noise formulation of the Skorokhod integral, cf. e.g. [a10]. Also, using instead of
. Thus, (a7) is an extension of Itô's integral to anticipating processes. Clearly, also the first term on the right-hand side of (a7) alone is an extension of the Itô-integral to non-adapted processes and it is the white noise formulation of the Skorokhod integral, cf. e.g. [a10]. Also, using instead of 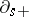 an analogous operator
an analogous operator 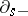 , one obtains (an extension of) the Itô backward integral and the mean of both is (an extension of) the Stratonovich integral [a9], [a3], [a12].
, one obtains (an extension of) the Itô backward integral and the mean of both is (an extension of) the Stratonovich integral [a9], [a3], [a12].
It has been shown in [a3] that Itô's lemma holds for the extended forward integral in its usual form (cf. also [a11]). The proof is completely based on Fock space methods, i.e. (a3). For the calculus of the Skorokhod integral, cf. [a2], [a10], [a12].
Generalizations.
Clearly one can define in the above way stochastic integrals (more precisely, stochastic differential forms) for processes with multi-dimensional time, or even with time parameter on manifolds, etc.
Also, instead of the symmetric Fock space one may work with the anti-symmetric Fock space over 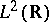 (or any other suitable Hilbert space of functions) and use operators
(or any other suitable Hilbert space of functions) and use operators 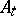 ,
, 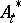 which fulfil the canonical anti-commutation relations
which fulfil the canonical anti-commutation relations
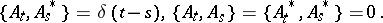 | (a8) |
This way one arrives at the fermionic stochastic integration and its calculus, see e.g. [a1], [a4]. In particular, one may define a fermionic Brownian motion as 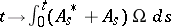 where
where  is the Fock space vacuum
is the Fock space vacuum 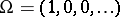 .
.
It is also possible to consider stochastic Volterra integral operators (cf. also Volterra equation)
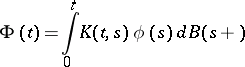 |
with stochastic kernel 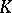 .
.
References
| [a1] | D. Applebaum, R.L. Hudson, "Fermion diffusions" J. Math. Phys. , 25 (1984) pp. 858–861 |
| [a2] | J. Asch, J. Potthoff, "A generalization of Itô's lemma" Proc. Japan Acad. , 63A (1987) pp. 289–291 |
| [a3] | J. Asch, J. Potthoff, "Itô's lemma without non-anticipatory conditions" Probab. Th. Rel. Fields , 88 (1991) pp. 17–46 |
| [a4] | C. Barnett, R.F. Streater, I.F. Wilde, "The Itô–Clifford integral" J. Funct. Anal. , 48 (1982) pp. 172–212 |
| [a5] | T. Hida, "Brownian motion" , Springer (1980) |
| [a6] | T. Hida, H.-H. Kuo, J. Potthoff, L. Streit, "White noise: An infinite dimensional calculus" , Kluwer Acad. Publ. (1993) |
| [a7] | I. Kubo, S. Takenaka, "Calculus on Gaussian white noise, I–IV" Proc. Japan Acad. , 56–58 (1980–1982) pp. 376–380; 411–416; 433–437; 186–189 |
| [a8] | H.-H. Kuo, "Brownian functionals and applications" Acta Applic. Math. , 1 (1983) pp. 175–188 |
| [a9] | H.-H. Kuo, A. Russek, "White noise approach to stochastic integration" J. Multivariate Anal. , 24 (1988) pp. 218–236 |
| [a10] | D. Nualart, E. Pardoux, "Stochastic calculus with anticipating integrands" Th. Rel. Fields , 78 (1988) pp. 535–581 |
| [a11] | J. Potthoff, "Stochastic integration in Hida's white noise calculus" S. Albeverio (ed.) D. Merlini (ed.) , Stochastic Processes, Physics and Geometry (1988) |
| [a12] | F. Russo, P. Vallois, "Forward, backward and symmetric stochastic integration" Probab. Th. Rel. Fields , 97 (1993) pp. 403–421 |
Stochastic integration via the Fock space of white noise. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stochastic_integration_via_the_Fock_space_of_white_noise&oldid=12828