Stiefel-Whitney class
A characteristic class with values in  , defined for real vector bundles. The Stiefel–Whitney classes are denoted by
, defined for real vector bundles. The Stiefel–Whitney classes are denoted by  ,
,  , and for a real vector bundle
, and for a real vector bundle 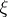 over a topological space
over a topological space  , the class
, the class  lies in
lies in  . These classes were introduced by E. Stiefel [1] and H. Whitney [2] and have the following properties. 1) For two real vector bundles
. These classes were introduced by E. Stiefel [1] and H. Whitney [2] and have the following properties. 1) For two real vector bundles  over a common base,
over a common base,
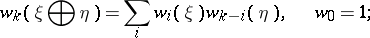 |
in other words,  , where
, where  is the complete Stiefel–Whitney class. 2) For the one-dimensional universal bundle
is the complete Stiefel–Whitney class. 2) For the one-dimensional universal bundle  over
over 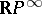 the equality
the equality  holds, where
holds, where  is the non-zero element of the group
is the non-zero element of the group  . These two properties together with naturality for induced bundles define the Stiefel–Whitney classes uniquely. The Stiefel–Whitney classes are stable, i.e.
. These two properties together with naturality for induced bundles define the Stiefel–Whitney classes uniquely. The Stiefel–Whitney classes are stable, i.e. 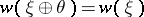 , where
, where 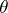 is the trivial bundle, and
is the trivial bundle, and  for
for 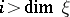 . For an oriented
. For an oriented  -dimensional vector bundle
-dimensional vector bundle 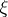 over a base
over a base  ,
, 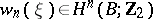 coincides with the reduction modulo 2 of the Euler class.
coincides with the reduction modulo 2 of the Euler class.
For a vector bundle 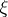 over
over  , let
, let 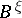 be the Thom space of this bundle. Further, let
be the Thom space of this bundle. Further, let  be the Thom isomorphism. Then the complete Stiefel–Whitney class
be the Thom isomorphism. Then the complete Stiefel–Whitney class 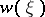 coincides with
coincides with
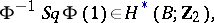 |
where  is the complete Steenrod square. This property of Stiefel–Whitney classes can be used as their definition. Stiefel–Whitney classes are homotopy invariants in the sense that they coincide for fibre-wise homotopically-equivalent bundles over a common base.
is the complete Steenrod square. This property of Stiefel–Whitney classes can be used as their definition. Stiefel–Whitney classes are homotopy invariants in the sense that they coincide for fibre-wise homotopically-equivalent bundles over a common base.
Any characteristic class with values in  , defined for real vector bundles, can be expressed by Stiefel–Whitney classes: The rings
, defined for real vector bundles, can be expressed by Stiefel–Whitney classes: The rings 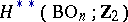 and
and 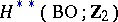 are rings of formal power series in the Stiefel–Whitney classes:
are rings of formal power series in the Stiefel–Whitney classes:
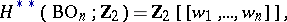 |
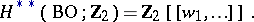 |
References
| [1] | E. Stiefel, "Richtungsfelden und Fernparallelismus in  -dimensionalen Mannigfaltigkeiten" Comm. Math. Helv. , 8 : 4 (1935–1936) pp. 305–353 -dimensionalen Mannigfaltigkeiten" Comm. Math. Helv. , 8 : 4 (1935–1936) pp. 305–353 |
| [2] | H. Whitney, "Topological properties of differentiable manifolds" Bull. Amer. Math. Soc. , 43 (1937) pp. 785–805 |
| [3] | J.W. Milnor, J.D. Stasheff, "Characteristic classes" , Princeton Univ. Press (1974) |
| [4] | R.E. Stong, "Notes on cobordism theory" , Princeton Univ. Press (1968) |
| [5] | N.E. Steenrod, "The topology of fibre bundles" , Princeton Univ. Press (1951) |
Comments
The notation 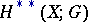 denotes the product of the Abelian groups
denotes the product of the Abelian groups  , while
, while  is the direct sum; the notation
is the direct sum; the notation  means that there is a graded homomorphism of degree
means that there is a graded homomorphism of degree  :
:  . For the classifying spaces
. For the classifying spaces  and
and  see Classifying space.
see Classifying space.
References
| [a1] | D. Husemoller, "Fibre bundles" , McGraw-Hill (1966) |
Stiefel-Whitney class. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stiefel-Whitney_class&oldid=12435