Steepest descent, method of
A special instance of the method of descent (cf. Descent, method of), when the direction 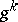 of descent is chosen as the direction opposite to
of descent is chosen as the direction opposite to 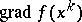 . The formulas of the method of steepest descent are
. The formulas of the method of steepest descent are
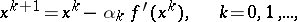 |
where the parameters 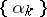 are determined by the condition that the function
are determined by the condition that the function 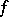 has maximum decrease at each step. If
has maximum decrease at each step. If 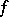 is twice continuously-differentiable and its matrix of second derivatives
is twice continuously-differentiable and its matrix of second derivatives 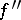 satisfies the inequality
satisfies the inequality
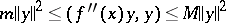 |
for any 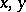 , with constants
, with constants 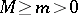 , then (see [2], [4]) the sequence
, then (see [2], [4]) the sequence 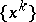 converges to a solution
converges to a solution 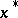 of the problem of minimizing
of the problem of minimizing 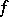 , the convergence rate being that of a geometric progression with quotient
, the convergence rate being that of a geometric progression with quotient 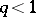 .
.
The method of steepest descent has been widely applied to the solution of systems of linear algebraic equations 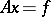 with a Hermitian or positive-definite matrix
with a Hermitian or positive-definite matrix 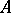 . In the real symmetric case, the problem of solving this system is equivalent to finding a vector
. In the real symmetric case, the problem of solving this system is equivalent to finding a vector 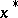 in an
in an  -dimensional vector space minimizing the functional
-dimensional vector space minimizing the functional
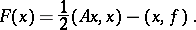 | (*) |
Applied to (*), the method of steepest descent takes the form
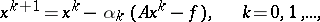 |
where the value of 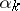 is determined by minimization of the functional (*), according to the formula
is determined by minimization of the functional (*), according to the formula
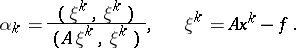 |
If the spectrum of 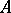 lies in an interval
lies in an interval 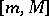 ,
, 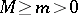 , on the real axis, then the sequence
, on the real axis, then the sequence 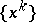 converges to the solution
converges to the solution 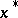 at the rate of a geometric progression with quotient
at the rate of a geometric progression with quotient 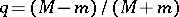 .
.
The method of steepest descent can be applied to solve an operator equation 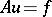 with a self-adjoint positive-definite bounded operator
with a self-adjoint positive-definite bounded operator 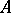 . If
. If 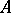 does not satisfy these conditions, the problem can be symmetrized, reduced to the problem
does not satisfy these conditions, the problem can be symmetrized, reduced to the problem
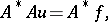 |
and then one can apply the method of steepest descent (see also Minimal discrepancy method).
References
| [1] | L.V. Kantorovich, "On the method of steepest descent" Dokl. Akad. Nauk SSSR , 56 : 3 (1947) pp. 233–236 (In Russian) |
| [2] | L.V. Kantorovich, G.P. Akilov, "Functional analysis" , Pergamon (1982) (Translated from Russian) |
| [3] | D.K. Faddeev, V.N. Faddeeva, "Computational methods of linear algebra" , Freeman (1963) (Translated from Russian) |
| [4] | B.N. Pshenichnyi, Yu.M. Danilin, "Numerical methods in extremal problems" , MIR (1978) (Translated from Russian) |
| [5] | N.S. Bakhvalov, "Numerical methods: analysis, algebra, ordinary differential equations" , MIR (1977) (Translated from Russian) |
Comments
References
| [a1] | G.H. Golub, C.F. van Loan, "Matrix computations" , Johns Hopkins Univ. Press (1989) |
Steepest descent, method of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Steepest_descent,_method_of&oldid=13529