Steenrod square
A stable cohomology operation  ,
,  , of the type
, of the type  , which raises the dimension by
, which raises the dimension by  . This means that for every integer
. This means that for every integer  and every pair of topological spaces
and every pair of topological spaces  , a homomorphism
, a homomorphism
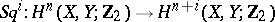 |
is defined such that  , where
, where  is the coboundary homomorphism
is the coboundary homomorphism 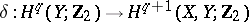 (stability) and
(stability) and 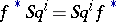 for any continuous mapping
for any continuous mapping 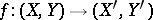 (naturality). The Steenrod squares
(naturality). The Steenrod squares 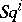 possess the following properties:
possess the following properties:
1) 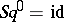 ;
;
2) 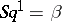 , where
, where 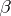 is the Bockstein homomorphism associated with the short exact sequence of coefficient groups
is the Bockstein homomorphism associated with the short exact sequence of coefficient groups 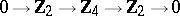 ;
;
3) if  , then
, then 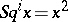 ;
;
4) if 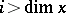 , then
, then  ;
;
5) (Cartan's formula) 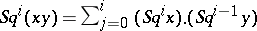 ;
;
6) (Adem relation) if 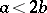 , then
, then
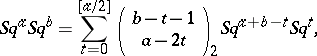 |
where  are binomial coefficients modulo 2.
are binomial coefficients modulo 2.
In Cartan's formula, multiplication can be considered as outer ( -multiplication) as well as interior (cup-multiplication). This is equivalent to the statement that the mapping
-multiplication) as well as interior (cup-multiplication). This is equivalent to the statement that the mapping 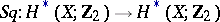 , defined by the formula
, defined by the formula
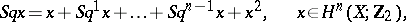 |
is a ring homomorphism. It follows from the stability condition that the Steenrod squares 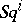 commute with suspension and transgression.
commute with suspension and transgression.
The properties 1), 3) and 4) define the operations 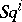 uniquely and can therefore be taken as defining axioms. The constructive definition of
uniquely and can therefore be taken as defining axioms. The constructive definition of 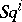 is based on the simplicial structure in chain groups
is based on the simplicial structure in chain groups 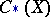 and on the existence of a diagonal mapping
and on the existence of a diagonal mapping 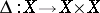 . Let
. Let 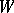 be the minimal acyclic free chain
be the minimal acyclic free chain  -complex i.e. the chain complex for which
-complex i.e. the chain complex for which
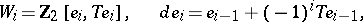 |
where 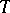 is the generator of
is the generator of 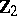 . The existence of an equivariant chain mapping
. The existence of an equivariant chain mapping
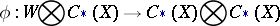 |
such that
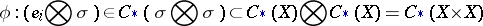 |
for any simplex 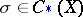 , is proved by the method of acyclic carriers or by an explicit construction (see [4]). The symbol
, is proved by the method of acyclic carriers or by an explicit construction (see [4]). The symbol 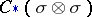 here signifies the smallest subcomplex of the chain complex
here signifies the smallest subcomplex of the chain complex 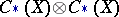 containing the element
containing the element 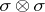 . Let
. Let 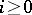 . Any two cochains
. Any two cochains 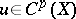 ,
, 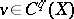 are put in correspondence by the formula
are put in correspondence by the formula 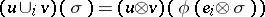 , for any simplex
, for any simplex 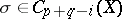 , with the cochain
, with the cochain 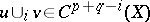 , which is called their cup-
, which is called their cup- -product. For the coboundary of this chain, the formula
-product. For the coboundary of this chain, the formula
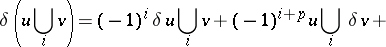 |
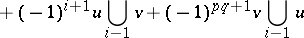 |
holds, from which it follows that the formula 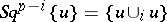 correctly defines a homomorphism
correctly defines a homomorphism
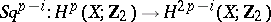 |
which does not depend on the choice of the mapping 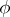 .
.
The operations 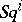 are constructed in the same way in other simplicial structures with a diagonal mapping, for example, in cohomology groups of simplicial Abelian groups, of simplicial Lie algebras, etc. However, not all properties of the Steenrod squares
are constructed in the same way in other simplicial structures with a diagonal mapping, for example, in cohomology groups of simplicial Abelian groups, of simplicial Lie algebras, etc. However, not all properties of the Steenrod squares 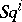 are preserved then (for example, generally speaking,
are preserved then (for example, generally speaking, 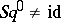 ) and there is yet (1991) no single general theory for the generalized operations
) and there is yet (1991) no single general theory for the generalized operations 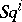 (see [5], [6]).
(see [5], [6]).
Many cohomology operations which act on cohomology groups with coefficients in the groups 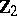 and
and 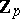 can be expressed in terms of the Steenrod squares and their analogues (see Steenrod reduced power). This underlines the fundamental role played by Steenrod squares in algebraic topology and its applications. For example, bordism groups are calculated using Steenrod squares.
can be expressed in terms of the Steenrod squares and their analogues (see Steenrod reduced power). This underlines the fundamental role played by Steenrod squares in algebraic topology and its applications. For example, bordism groups are calculated using Steenrod squares.
Steenrod squares were introduced by N. Steenrod [4].
References
| [1] | N.E. Steenrod, D.B.A. Epstein, "Cohomology operations" , Princeton Univ. Press (1962) |
| [2] | D.B. Fuks, A.T. Fomenko, V.L. Gutenmakher, "Homotopic topology" , Moscow (1969) (In Russian) |
| [3] | M.K. Tangora, "Cohomology operations and applications in homotopy theory" , Harper & Row (1968) |
| [4] | N.E. Steenrod, "Products of cocylces and extensions of mappings" Ann. of Math. , 48 (1947) pp. 290–320 |
| [5] | D. Epstein, "Steenrod operations in homological algebra" Invent. Math. , 1 : 2 (1966) pp. 152–208 |
| [6] | J. May, "A general algebraic approach to Steenrod operations" , The Steenrod Algebra and Its Applications , Lect. notes in math. , 168 , Springer (1970) pp. 153–231 |
| [7] | Matematika , 5 : 2 (1961) pp. 3–11; 11–30; 30–49; 50–102 |
Comments
References
| [a1] | J. Dieudonné, "A history of algebraic and differential topology 1900–1960" , Birkhäuser (1989) |
| [a2] | R.M. Switzer, "Algebraic topology - homotopy and homology" , Springer (1975) pp. Chapt. 18 |
| [a3] | J.F. Adams, "Stable homotopy and generalised homology" , Univ. Chicago Press (1974) pp. Part III, Chapt. 12 |
| [a4] | E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) pp. Chapt. V, Sect. 9 |
Steenrod square. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Steenrod_square&oldid=48827