Statistical acceptance control
The branch of statistical quality control of industrial mass production aimed at showing that the product conforms to certain requirements. In the USSR, statistical acceptance control is based on State Standards. These contain tables of control plans and rules governing the choice of plans from these tables. The control can be carried out with different degrees of strictness. When choosing the control plan and the degree of strictness, account must be taken of the size of the lot to be controlled (i.e. the number of items it contains), the results of the control of previous lots and other factors. Statistical acceptance control is an effective method of maintaining the required level of production quality.
Two kinds of statistical acceptance control are most often used: control through an alternative characteristic and control through a quantitative characteristic. In the former, items are classified as acceptable or defective; in the latter, real-valued parameters of the items are measured.
Various methods are used in selecting items for control. One which is widely used is random choice without replacement (see Sample method), whereby all samples of the same size have equal probabilities. If the control is of a destructive nature (a disruption test), then a complete inspection is impossible. Using statistical acceptance control, it is generally possible to test only some of the items in the sample, which means that false decisions may ensue. In the theory of statistical acceptance control, methods are devised to calculate the probabilistic characteristics of the control plans and to estimate the efficiency of the control on the basis of the information compiled during the control process.
Statistical acceptance control is often carried out using one-stage plans. Let 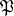 be the lot of
be the lot of 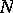 items being inspected. A one-stage plan is characterized by the fact that it defines the size
items being inspected. A one-stage plan is characterized by the fact that it defines the size  of the sample and that it uses the acceptance number
of the sample and that it uses the acceptance number  . If the number of defective items in the sample proves to be equal to
. If the number of defective items in the sample proves to be equal to  and
and 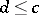 , then
, then 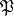 is accepted. If
is accepted. If 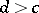 , however, then
, however, then 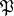 is rejected. Depending on what kind of item is being inspected, the decision of rejecting can either entail a complete inspection of all items from
is rejected. Depending on what kind of item is being inspected, the decision of rejecting can either entail a complete inspection of all items from 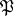 that are not included in the sample, or a reduction in the number of distinct types, etc. The USSR State Standards make use of two-stage, multi-stage and sequential plans. A two-stage plan is defined by the sizes
that are not included in the sample, or a reduction in the number of distinct types, etc. The USSR State Standards make use of two-stage, multi-stage and sequential plans. A two-stage plan is defined by the sizes 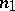 and
and 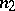 of the first and second samples, by the acceptance numbers
of the first and second samples, by the acceptance numbers 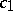 ,
, 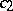 , and by the rejection numbers
, and by the rejection numbers 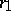 ,
, 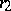 (
(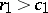 ,
,  ). If the number of defective items in the first sample
). If the number of defective items in the first sample 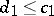 , then
, then 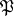 is accepted. If
is accepted. If 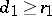 , then
, then 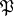 is rejected. When
is rejected. When 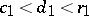 , a second sample is taken. If
, a second sample is taken. If 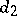 is the number of defective items in the second sample and
is the number of defective items in the second sample and 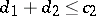 , then
, then 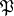 is accepted. If
is accepted. If 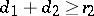 , then
, then 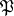 is rejected.
is rejected.
One important numerical characteristic of statistical acceptance control plans using a control through an alternative characteristic is the operating characteristic 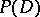 , which is equal to the probability of a lot being accepted according to the results of the inspection of the items in the sample. For a one-stage plan
, which is equal to the probability of a lot being accepted according to the results of the inspection of the items in the sample. For a one-stage plan
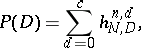 |
where
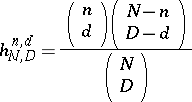 |
is the probability of discovering 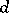 defective items in a random sample of size
defective items in a random sample of size  , without replacement, when
, without replacement, when 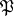 contains
contains 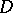 effective items. The distribution with probabilities
effective items. The distribution with probabilities 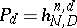 ,
, 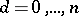 , is called hypergeometric (cf. Hypergeometric distribution). Numerical characteristics of control plans are often calculated by approximating the hypergeometric distribution by a binomial or Poisson distribution (cf. Binomial distribution; Poisson distribution). For two-stage and sequential plans, the average number of controlled items
, is called hypergeometric (cf. Hypergeometric distribution). Numerical characteristics of control plans are often calculated by approximating the hypergeometric distribution by a binomial or Poisson distribution (cf. Binomial distribution; Poisson distribution). For two-stage and sequential plans, the average number of controlled items 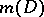 is an essential characteristic.
is an essential characteristic.
The USSR State Tables of control plans contain parameters of plans that possess (at least approximately) different properties of optimality. Let 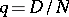 be the proportion of defective items, and let
be the proportion of defective items, and let 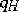 be the average proportion of defective items in the stationary process of production. Optimal control plans are to be found among plans with identical expected expenditure when
be the average proportion of defective items in the stationary process of production. Optimal control plans are to be found among plans with identical expected expenditure when 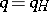 . The expected expenditure is equal to the cost of inspecting the items in the sample and the loss incurred by wrongly rejecting acceptable items. It is sometimes advisable to include losses incurred by accepting defective items in the expenditure. The USSR State Standards [1] contain tables of one-stage plans which, given a definite expected level of expenditure on the control and a definite
. The expected expenditure is equal to the cost of inspecting the items in the sample and the loss incurred by wrongly rejecting acceptable items. It is sometimes advisable to include losses incurred by accepting defective items in the expenditure. The USSR State Standards [1] contain tables of one-stage plans which, given a definite expected level of expenditure on the control and a definite 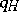 , provide the consumer with the approximately best-possible defence against the acceptance of lots containing
, provide the consumer with the approximately best-possible defence against the acceptance of lots containing 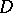 defective items in a wide range of values
defective items in a wide range of values 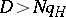 . This means that the operating characteristics of these plans for a wide range of values of
. This means that the operating characteristics of these plans for a wide range of values of 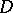 are close to the lower envelope of the operating characteristics of all one-stage plans which, when
are close to the lower envelope of the operating characteristics of all one-stage plans which, when 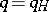 , have identical expected expenditure on control. Constructing the tables in the USSR State Standards requires a great deal of computer time.
, have identical expected expenditure on control. Constructing the tables in the USSR State Standards requires a great deal of computer time.
The use of the results of statistical acceptance control of many lots of products may lead to so-called successive estimators of different quantities that reflect the efficiency of the standard being used. For example, unbiased estimators can be found for the total number of defective items in the lots subjected to control. Control by one-stage plans may lead to estimators of the total number of defective items accepted by the consumer. The bias in these estimators quickly diminishes as the sizes of the samples increase. The use of successive estimators in statistical acceptance control was proposed by A.N. Kolmogorov [2]. Various generalizations are known for methods of statistical acceptance control through an alternative characteristic (see [3], [4]); in certain of its applications, it is advisable to examine a statistical acceptance control that allows an erroneous classification of defective items as acceptable, and vice versa [5]. Bayesian methods are widely used [6] (cf. also Bayesian approach).
Standards for statistical acceptance control through a quantitative characteristic are based on the fact that the characteristics of the items in the sample which can be measured in the control are mutually-independent identically-distributed random variables with distribution functions that belong to a certain parametric family. The standards most frequently used are those in which normal (Gaussian) distributions form such a family. In practice, checking the above conditions requires exhaustive testing, and must precede a decision on which standard to use for statistical acceptance control through a quantitative characteristic.
Only when the use of statistical sampling control through a quantitative characteristic is justified can results be obtained that are more effective than those provided by statistical acceptance control through an alternative characteristic.
References
| [1] | , GOST 24660–81 (Russian State Standards for quality control) |
| [2] | A.N. Kolmogorov, "Unbiased estimators" Izv. Akad. Nauk SSSR Ser. Mat. , 14 : 4 (1950) pp. 303–326 (In Russian) |
| [3] | Yu.K. Belyaev, "Probabilistic methods of sample control" , Moscow (1975) (In Russian) |
| [4] | Ya.P. Lumel'skii, "Statistical estimators of the results of quality control" , Moscow (1979) (In Russian) |
| [5] | Yu.K. Belyaev, "Sequential estimates in sampling inspection by means of a qualitative criterion with classification errors" Soviet Math. Dokl. , 17 : 6 (1976) pp. 1572–1576 Dokl. Akad. Nauk SSSR , 231 : 3 (1976) pp. 521–524 |
| [6] | A. Hald, "Statistical theory of sampling inspection by attributes" , 1–2 , Univ. Copenhagen (1981) |
Comments
References
| [a1] | J.M. Juran (ed.) , Quality control handbook , McGraw-Hill (1962) |
Statistical acceptance control. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Statistical_acceptance_control&oldid=17177