Stability of characteristic exponents
A property of the (Lyapunov) characteristic exponents (cf. Lyapunov characteristic exponent) of a linear system of ordinary differential equations
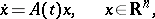 | (1) |
where 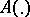 is a continuous mapping
is a continuous mapping 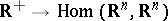 (or
(or 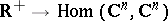 ), satisfying the condition
), satisfying the condition
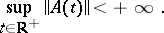 |
One says that the characteristic exponents of the system (1) are stable if each of the functions
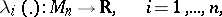 |
is continuous at the point 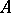 . Here
. Here 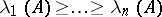 are the characteristic exponents of the system (1) and
are the characteristic exponents of the system (1) and 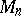 is the set of all systems (1), equipped with the structure of a metric space given by the distance
is the set of all systems (1), equipped with the structure of a metric space given by the distance
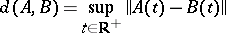 |
(for convenience the system (1) is identified with the mapping  ; moreover, instead of
; moreover, instead of  one writes
one writes 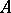 ).
).
Systems (1) with unstable exponents have been found (cf. [2], [3]). For example, the characteristic exponents of the system
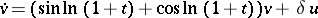 |
for 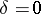 are unstable, since for
are unstable, since for 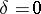 the largest characteristic exponent
the largest characteristic exponent 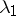 is 1, and for
is 1, and for 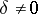 ,
, 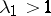 and
and 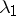 does not depend on
does not depend on 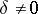 . For the stability of the characteristic exponents it is sufficient that the integral separation condition should be fulfilled (Perron's theorem). The set of systems (1) satisfying this condition coincides with the interior (in the space
. For the stability of the characteristic exponents it is sufficient that the integral separation condition should be fulfilled (Perron's theorem). The set of systems (1) satisfying this condition coincides with the interior (in the space 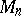 ) of the set of all systems (1) with stable characteristic exponents.
) of the set of all systems (1) with stable characteristic exponents.
If 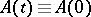 for all
for all 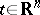 or
or 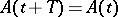 for all
for all 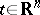 (for a certain
(for a certain 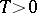 ) (i.e. the system (1) has constant or periodic coefficients), then the characteristic exponents of the system (1) are stable. If
) (i.e. the system (1) has constant or periodic coefficients), then the characteristic exponents of the system (1) are stable. If 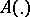 is an almost-periodic mapping (cf. Linear system of differential equations with almost-periodic coefficients), then for the stability of the characteristic exponents of the system (1) it is necessary and sufficient that the system (1) be almost reducible (cf. also Reducible linear system).
is an almost-periodic mapping (cf. Linear system of differential equations with almost-periodic coefficients), then for the stability of the characteristic exponents of the system (1) it is necessary and sufficient that the system (1) be almost reducible (cf. also Reducible linear system).
For the characteristic exponents of the system (1) to be stable it is sufficient that there is a Lyapunov transformation reducing the system (1) to block-diagonal form:
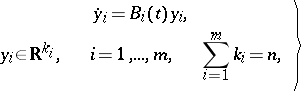 | (2) |
such that: a) the blocks are integrally separable, i.e. numbers 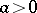 ,
, 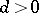 can be found such that
can be found such that
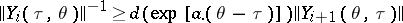 |
for all 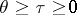 ,
, 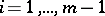 (here
(here 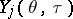 is the Cauchy operator for the system (2)); and b) the upper and lower central exponents of the system (2) are equal to each other:
is the Cauchy operator for the system (2)); and b) the upper and lower central exponents of the system (2) are equal to each other:
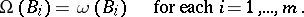 |
The conditions of this theorem are also necessary for the stability of the characteristic exponents of the system (1) (cf. [6]). Systems with unstable characteristic exponents may possess the property of stochastic stability of the characteristic exponents.
The characteristic exponents of the system (1) are called stochastically stable (or almost-certainly stable) if for  the characteristic exponents of the system
the characteristic exponents of the system
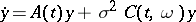 |
tend with probability 1 to the characteristic exponents of the system (1); here the elements of the matrix giving the linear operator 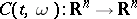 (in a certain basis of
(in a certain basis of 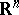 which is independent of
which is independent of 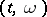 ) are independent non-null white noise.
) are independent non-null white noise.
If the mapping  is uniformly continuous and if
is uniformly continuous and if
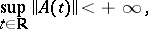 |
then for almost-every mapping 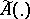 , where
, where
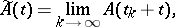 |
the characteristic exponents of the system 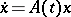 are stochastically stable (for the shift dynamical system
are stochastically stable (for the shift dynamical system  one considers a normalized invariant measure, concentrated on the closure of the trajectory of the point
one considers a normalized invariant measure, concentrated on the closure of the trajectory of the point 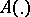 ; by "almost-every A" one means almost-every
; by "almost-every A" one means almost-every 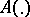 in the sense of each such measure).
in the sense of each such measure).
Let a dynamical system on a smooth closed manifold 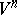 be given by a smooth vector field. Then for almost-every point
be given by a smooth vector field. Then for almost-every point 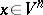 (in the sense of each normalized invariant measure) the characteristic exponents of the system of variational equations associated with the trajectory of the point
(in the sense of each normalized invariant measure) the characteristic exponents of the system of variational equations associated with the trajectory of the point  are stochastically stable.
are stochastically stable.
References
| [1] | A.M. Lyapunov, "Stability of motion" , Acad. Press (1966) (Translated from Russian) |
| [2] | O. Perron, "Die Ordnungszahlen der Differentialgleichungssysteme" Math. Z. , 31 (1930) pp. 748–766 |
| [3] | O. Perron, "Ueber lineare Differentialgleichungen, bei denen die unabhängig Variable reel ist I" J. Reine Angew. Math. , 142 (1913) pp. 254–270 |
| [4] | V.V. Nemytskii, V.V. Stepanov, "Qualitative theory of differential equations" , Princeton Univ. Press (1960) (Translated from Russian) |
| [5] | B.F. Bylov, R.E. Vinograd, D.M. Grobman, V.V. Nemytskii, "The theory of Lyapunov exponents and its applications to problems of stability" , Moscow (1966) (In Russian) |
| [6] | N.A. Izobov, "Linear systems of ordinary differential equations" J. Soviet Math. , 5 : 1 (1976) pp. 46–96 Itogi Nauk. i Tekhn. Mat. Anal. , 12 (1974) pp. 71–146 |
Stability of characteristic exponents. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stability_of_characteristic_exponents&oldid=18227