Stability in game theory

A principle reflecting directly or indirectly the idea of stability of a situation (or of a set of situations). One singles out the following basic concepts of stability.

1) 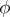-stability, cf. Coalitional game.

2) 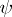-stability. An optimality principle in a cooperative game, connected with the concept of stability of pairs, consisting of a partition of the set 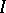of players into coalitions and allocations relative to the formation of new coalitions. A partition 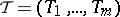of the set 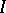of players is called a coalition structure. Let 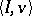be a cooperative game and 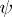a function associating with every coalition structure 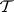a set of coalitions 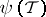. 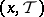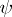A pair , where is an allocation, is called -stable if 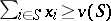for all 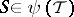and if 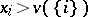when .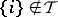

3) 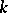-stability. A special case of 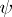-stability, when for 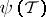a set of coalitions is chosen, each of which differs from any element of 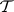by not more than 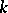players.

4) 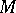-stability. An optimality principle in the theory of cooperative games which formalizes the intuitive notion of stability of formation of coalitions and allocation of values 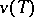of a characteristic function defined on the set of coalitions 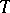relative to the possible threat of one coalition against the others. A pair 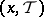, where 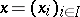is a vector satisfying the condition 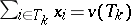, , 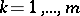while 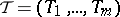is a coalition structure, is called a configuration. A configuration is said to be individually rational if , . A configuration is called coalitionally rational if the vector satisfies 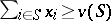for any coalition 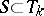, 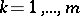. 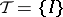In case , in particular when , for every individually rational configuration 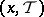the vector is an allocation.

The set 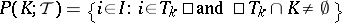is called the set of partners of a coalition 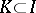in a coalition structure 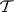. Let 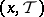be a coalitionally rational configuration and let 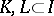be disjoint coalitions. A coalitionally rational configuration 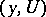satisfying the conditions

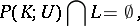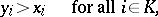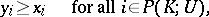is called a threat of a coalition 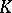against 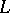. By a counter-threat of 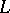against 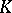one understands a coalitionally rational configuration 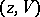satisfying the conditions

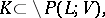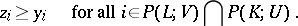A coalitionally rational configuration 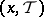is called 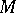-stable if for any pair of disjoint coalitions and for every threat of 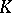against there is a counter-threat of 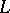against 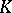. The set of all 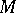-stable configurations for a coalition structure 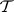is called the 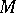-stable set and is denoted by or 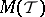. In the case 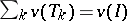, the set 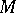contains the core (cf. Core in the theory of games) of the cooperative game 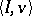. The set often turns out to be empty, and therefore one considers further the set 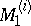which is defined analogously to 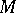, with the following changes: one considers not only coalitionally rational configurations, but all individually rational configurations admitting only threats and counter-threats among one-element coalitions, i.e. between individual players. It can be proved that the set 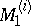is non-empty for any coalition structure. The set 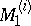for 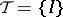contains the 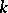-kernel and coincides with it and the core for a convex game .

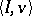The concepts of 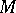-stability and 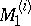-stability have a natural generalization to cooperative games without side payments. It is known that in this case the set 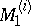may be empty; there are certain conditions for to be non-empty.

References

[1]	R.J. Aumann, M. Maschler, "The bargaining set for cooperative games" , Advances in game theory , Princeton Univ. Press pp. 443–476
[2]	N.N. Vorob'ev, "The present state of the theory of games" Russian Math. Surveys , 25 : 2 (1970) pp. 77–150 Uspekhi Mat. Nauk , 25 : 2 (1970) pp. 81–140
[3]	R.D. Luce, , Mathematical Models of Human Behaviour , Stanford (1955) pp. 32–44
[4]	R.D. Luce, H. Raiffa, "Games and decisions. Introduction and critical survey" , Wiley (1957)
[5]	B. Peleg, "Existence theorem for the bargaining of 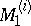" Bull. Amer. Math. Soc. , 69 (1963) pp. 109–110
[6]	B. Peleg, "Quota games with a continuum of players" Israel J. Math. , 1 (1963) pp. 48–53
[7]	G. Owen, "The theory of games" , Acad. Press (1982)