Splittable group
A group 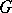 generated by proper subgroups
generated by proper subgroups 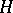 and
and 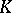 with
with 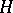 normal in
normal in 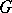 and
and 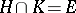 (so that the quotient group
(so that the quotient group 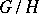 is isomorphic to
is isomorphic to 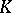 , cf. Normal subgroup).
, cf. Normal subgroup). 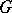 is called a split extension of the group
is called a split extension of the group 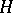 by the group
by the group 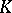 , or a semi-direct product of
, or a semi-direct product of 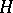 and
and 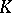 . If the subgroups
. If the subgroups 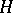 and
and 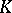 commute elementwise, i.e.
commute elementwise, i.e. 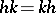 for all
for all 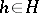 ,
, 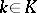 , their semi-direct product coincides with the direct product
, their semi-direct product coincides with the direct product 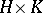 . A semi-direct product
. A semi-direct product 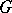 of a group
of a group 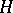 and a group
and a group 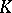 is given by a homomorphism
is given by a homomorphism 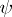 of
of 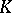 into the group
into the group  of automorphisms of
of automorphisms of 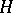 . In this case, the formula
. In this case, the formula
 |
for all 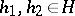 ,
, 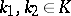 , defines the multiplication in
, defines the multiplication in 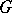 . In the case when
. In the case when 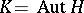 and
and 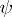 is the identity mapping,
is the identity mapping, 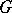 is called the holomorph of
is called the holomorph of 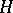 (cf. Holomorph of a group).
(cf. Holomorph of a group).
References
| [1] | D. Gorenstein, "Finite groups" , Chelsea, reprint (1980) |
Comments
Conversely, if 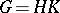 is a semi-direct product, then conjugation with
is a semi-direct product, then conjugation with 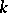 in
in  defines a homomorphism
defines a homomorphism  from which
from which 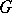 can be reconstructed, i.e.
can be reconstructed, i.e.
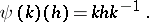 |
As a set the semi-direct product of 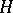 and
and 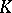 is
is 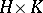 . The subsets
. The subsets 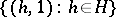 ,
, 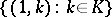 are subgroups that identify with
are subgroups that identify with 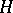 and
and 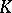 .
.
Splittable group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Splittable_group&oldid=14172