Spherical harmonics
of degree 
A restriction of a homogeneous harmonic polynomial  of degree
of degree  in
in  variables
variables  to the unit sphere
to the unit sphere  of the Euclidean space
of the Euclidean space  ,
,  . In particular, when
. In particular, when 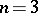 , the spherical harmonics are the classical spherical functions.
, the spherical harmonics are the classical spherical functions.
Let 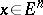 ,
,  ,
,  ,
, 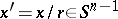 . The basic property of spherical harmonics is the property of orthogonality: If
. The basic property of spherical harmonics is the property of orthogonality: If  and
and 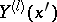 are spherical harmonics of degree
are spherical harmonics of degree 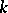 and
and  , respectively, with
, respectively, with  , then
, then
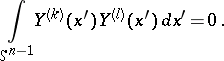 |
The simplest spherical harmonics are the zonal spherical harmonics. For any 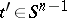 and any
and any 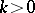 , a zonal spherical harmonic
, a zonal spherical harmonic  exists which is constant on any parallel of the sphere
exists which is constant on any parallel of the sphere  that is orthogonal to the vector
that is orthogonal to the vector  . The zonal spherical harmonics
. The zonal spherical harmonics 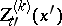 differ from the Legendre polynomials
differ from the Legendre polynomials 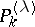 , when
, when 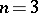 , or from the ultraspherical polynomials
, or from the ultraspherical polynomials 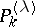 , when
, when 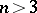 , only by a constant factor:
, only by a constant factor:
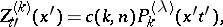 |
where the polynomials 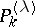 are defined, when
are defined, when  , by the generating function
, by the generating function
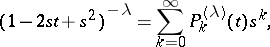 |
 ,
, 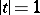 ,
, 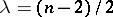 . The polynomials
. The polynomials 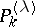 ,
, 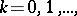 are orthogonal with weight
are orthogonal with weight 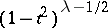 and form an orthogonal basis of the space
and form an orthogonal basis of the space 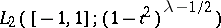 . If
. If  is a function in
is a function in  with
with 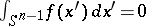 , then there is a unique set of spherical harmonics
, then there is a unique set of spherical harmonics 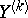 such that
such that
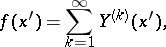 |
where the series converges in the norm of  .
.
Expansions in spherical harmonics are largely analogous to expansions in Fourier series, of which they are essentially a generalization. The homogeneous harmonic polynomials  are sometimes called spatial spherical harmonics. By virtue of the homogeneity
are sometimes called spatial spherical harmonics. By virtue of the homogeneity
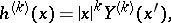 |
spherical harmonics are sometimes also called surface spherical harmonics.
References
| [1] | P.M. Morse, H. Feshbach, "Methods of theoretical physics" , 1–2 , McGraw-Hill (1953) |
| [2] | E.M. Stein, G. Weiss, "Introduction to Fourier analysis on Euclidean spaces" , Princeton Univ. Press (1971) |
Comments
References
| [a1] | I.M. Gel'fand, R.A. Minlos, Z.Ya. Shapiro, "Representations of the rotation group and the Lorentz group, and their applications" , Macmillan (1963) (Translated from Russian) |
| [a2] | N.Ya. Vilenkin, "Special functions and the theory of group representations" , Amer. Math. Soc. (1968) (Translated from Russian) |
| [a3] | N.Ya. Vilenkin, A.U. Klimyk, "Special functions, group representations, and integral transforms" , 1 , Kluwer (1991) (Translated from Russian) |
Spherical harmonics. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Spherical_harmonics&oldid=12872