Spherical functions
solid spherical harmonics, associated Legendre functions of the first and second kinds
Two linearly independent solutions  and
and  of the differential equation
of the differential equation
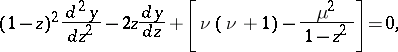 |
where  and
and  are complex constants, which arises in the solution of a class of partial differential equations by the method of separation of variables (cf. Separation of variables, method of). The points
are complex constants, which arises in the solution of a class of partial differential equations by the method of separation of variables (cf. Separation of variables, method of). The points  are branching points of the solutions, in general. The spherical functions are particular cases of the hypergeometric functions (cf. Hypergeometric function):
are branching points of the solutions, in general. The spherical functions are particular cases of the hypergeometric functions (cf. Hypergeometric function):
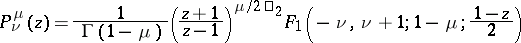 |
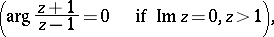 |
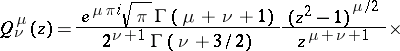 |
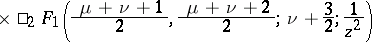 |
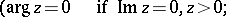 |
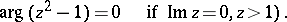 |
The spherical functions 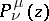 and
and 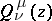 are defined and single-valued in the domains
are defined and single-valued in the domains 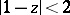 and
and 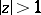 , respectively, of the complex plane cut by the real axis from
, respectively, of the complex plane cut by the real axis from 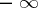 to
to 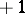 .
.
If  ,
,  ,
, 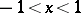 , then the following functions are usually taken as solutions:
, then the following functions are usually taken as solutions:
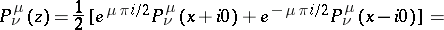 |
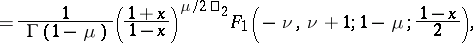 |
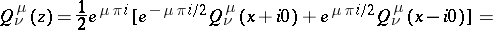 |
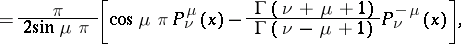 |
where 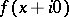
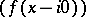 are the values of the function
are the values of the function  on the upper (lower) boundary of the cut.
on the upper (lower) boundary of the cut.
When  ,
, 
 are the Legendre polynomials. For zonal spherical functions see Spherical harmonics.
are the Legendre polynomials. For zonal spherical functions see Spherical harmonics.
References
| [1] | H. Bateman (ed.) A. Erdélyi (ed.) et al. (ed.) , Higher transcendental functions , 2. Bessel functions, parabolic cylinder functions, orthogonal polynomials , McGraw-Hill (1953) |
| [2] | E. Jahnke, F. Emde, "Tables of functions with formulae and curves" , Dover, reprint (1945) (Translated from German) |
| [3] | E.T. Whittaker, G.N. Watson, "A course of modern analysis" , Cambridge Univ. Press (1952) pp. Chapt. 6 |
| [4] | A. Krazer, W. Franz, "Transzendente Funktionen" , Akademie Verlag (1960) |
| [5] | E.W. Hobson, "The theory of spherical and ellipsoidal harmonics" , Chelsea, reprint (1955) |
Comments
A more common usage of the phrase "spherical function" is as follows.
Let 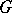 be a unimodular locally compact group and
be a unimodular locally compact group and 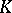 a subgroup of
a subgroup of 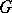 . Let
. Let 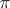 be an irreducible unitary representation of
be an irreducible unitary representation of 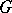 on a Hilbert space
on a Hilbert space  such that the
such that the 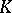 -fixed vectors in
-fixed vectors in  form a one-dimensional subspace, spanned by a unit vector
form a one-dimensional subspace, spanned by a unit vector  . Then the
. Then the 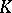 -bi-invariant function
-bi-invariant function 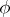 on
on 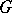 defined by
defined by 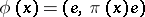 is called a spherical function. Sometimes
is called a spherical function. Sometimes  is called a zonal spherical function, while the functions
is called a zonal spherical function, while the functions  (
(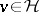 ) are also called spherical functions. Some authors call
) are also called spherical functions. Some authors call 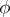 an elementary spherical function, while all
an elementary spherical function, while all 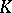 -bi-invariant functions on
-bi-invariant functions on 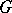 are called spherical functions.
are called spherical functions.
The pair 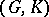 is a Gel'fand pair if, for all irreducible unitary representations of
is a Gel'fand pair if, for all irreducible unitary representations of 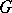 , the subspace of
, the subspace of  -fixed vectors in the representation space has dimension
-fixed vectors in the representation space has dimension 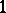 or
or  . This is equivalent to the commutativity of the convolution algebra
. This is equivalent to the commutativity of the convolution algebra 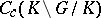 of
of 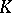 -bi-invariant continuous functions on
-bi-invariant continuous functions on 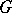 with compact support. Now spherical functions are more generally defined as solutions
with compact support. Now spherical functions are more generally defined as solutions 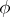 , not identically zero, of the functional equation
, not identically zero, of the functional equation
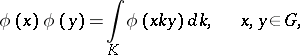 | (*) |
where 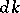 is the normalized Haar measure on
is the normalized Haar measure on  . These solutions include the spherical functions associated with irreducible unitary representations. Other solutions may be associated with irreducible non-unitary representations of
. These solutions include the spherical functions associated with irreducible unitary representations. Other solutions may be associated with irreducible non-unitary representations of  . The characters of the comutative algebra
. The characters of the comutative algebra 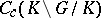 are precisely the mappings
are precisely the mappings 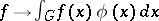 , where
, where 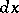 is Haar measure on
is Haar measure on 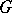 and
and  is a solution of (*).
is a solution of (*).
If  is, moreover, a connected Lie group, then
is, moreover, a connected Lie group, then 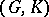 is a Gel'fand pair if and only if the algebra
is a Gel'fand pair if and only if the algebra  of
of 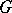 -invariant differential operators on the homogeneous space
-invariant differential operators on the homogeneous space  is commutative. Then
is commutative. Then 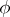 is a solution of (*) if and only if it is
is a solution of (*) if and only if it is  -bi-invariant,
-bi-invariant,  ,
, 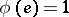 , and the function
, and the function  on
on  is a joint eigenfunction of the elements of
is a joint eigenfunction of the elements of  . In particular, if
. In particular, if 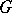 is a connected real semi-simple LIe group and
is a connected real semi-simple LIe group and 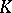 is a maximal compact subgroup, then
is a maximal compact subgroup, then  is a Gel'fand pair,
is a Gel'fand pair, 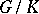 is a Riemannian symmetric space, and much information is available about
is a Riemannian symmetric space, and much information is available about 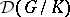 and the sperical functions.
and the sperical functions.
References
| [a1] | J. Fauraut, "Analyse harmonique sur les paires de Gelfand et les espaces hyperboliques" , Anal. Harmonique , CIMPA (1982) pp. 315–446 |
| [a2] | I.M. Gel'fand, "Spherical functions on symmetric spaces" Transl. Amer. Math. Soc. , 37 (1964) pp. 39–44 Dokl. Akad. Nauk SSSR , 70 (1950) pp. 5–8 |
| [a3] | R. Godement, "Introduction aux traveaux de A. Selberg" Sem. Bourbaki , 144 (1957) |
| [a4] | S. Helgason, "Groups and geometric analysis" , Acad. Press (1984) pp. Chapt. II, Sect. 4 |
Spherical functions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Spherical_functions&oldid=16632