Spectral theory of compact operators
From Encyclopedia of Mathematics
Riesz theory of compact operators
Let  be a complex Banach space and
be a complex Banach space and  a compact operator on
a compact operator on  . Then
. Then  , the spectrum of
, the spectrum of  , is countable and has no cluster points except, possibly,
, is countable and has no cluster points except, possibly,  . Every
. Every  is an eigenvalue, and a pole of the resolvent function
is an eigenvalue, and a pole of the resolvent function  . Let
. Let  be the order of the pole
be the order of the pole 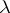 . For each
. For each 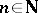 ,
,  is closed, and this range is constant for
is closed, and this range is constant for 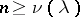 . The null space
. The null space 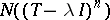 is finite dimensional and constant for
is finite dimensional and constant for 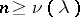 . The spectral projection
. The spectral projection 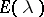 (the Riesz projector, see Riesz decomposition theorem) has non-zero finite-dimensional range, equal to
(the Riesz projector, see Riesz decomposition theorem) has non-zero finite-dimensional range, equal to  , and its null space is
, and its null space is 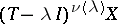 . Finally,
. Finally, 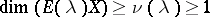 .
.
The respective integers 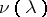 and
and 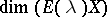 are called the index and the algebraic multiplicity of the eigenvalue
are called the index and the algebraic multiplicity of the eigenvalue 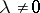 .
.
References
| [a1] | H.R. Dowson, "Spectral theory of linear operators" , Acad. Press (1978) pp. 45ff. |
| [a2] | N. Dunford, J.T. Schwartz, "Linear operators I: General theory" , Interscience (1964) pp. Sect. VII.4 |
How to Cite This Entry:
Spectral theory of compact operators. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Spectral_theory_of_compact_operators&oldid=18215
Spectral theory of compact operators. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Spectral_theory_of_compact_operators&oldid=18215
This article was adapted from an original article by M. Hazewinkel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article