Sobolev space
A space 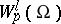 of functions
of functions 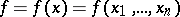 on a set
on a set 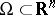 (usually open) such that the
(usually open) such that the  -th power of the absolute value of
-th power of the absolute value of 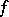 and of its generalized derivatives (cf. Generalized derivative) up to and including order
and of its generalized derivatives (cf. Generalized derivative) up to and including order 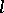 are integrable (
are integrable (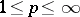 ).
).
The norm of a function 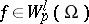 is given by
is given by
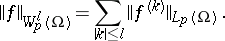 | (1) |
Here
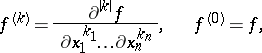 |
is the generalized partial derivative of 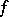 of order
of order 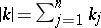 , and
, and
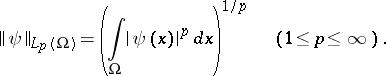 |
When 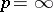 , this norm is equal to the essential supremum:
, this norm is equal to the essential supremum:
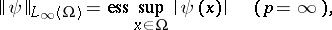 |
that is, to the greatest lower bound of the set of all 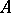 for which
for which 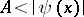 on a set of measure zero.
on a set of measure zero.
The space 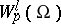 was defined and first applied in the theory of boundary value problems of mathematical physics by S.L. Sobolev (see [1], [2]).
was defined and first applied in the theory of boundary value problems of mathematical physics by S.L. Sobolev (see [1], [2]).
Since its definition involves generalized derivatives rather than ordinary ones, it is complete, that is, it is a Banach space.
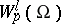 is considered in conjunction with the linear subspace
is considered in conjunction with the linear subspace 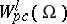 consisting of functions having partial derivatives of order
consisting of functions having partial derivatives of order 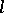 that are uniformly continuous on
that are uniformly continuous on  .
. 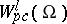 has advantages over
has advantages over 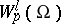 , although it is not closed in the metric of
, although it is not closed in the metric of 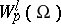 and is not a complete space. However, for a wide class of domains (those with a Lipschitz boundary, see below) the space
and is not a complete space. However, for a wide class of domains (those with a Lipschitz boundary, see below) the space 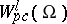 is dense in
is dense in 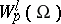 for all
for all 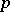 ,
, 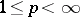 , that is, for such domains the space
, that is, for such domains the space 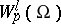 acquires a new property in addition to completeness, in that every function belonging to it can be arbitrarily well approximated in the metric of
acquires a new property in addition to completeness, in that every function belonging to it can be arbitrarily well approximated in the metric of  by functions from
by functions from 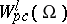 .
.
It is sometimes convenient to replace the expression (1) for the norm of 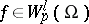 by the following:
by the following:
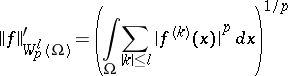 | (1prm) |
 |
The norm (1prm) is equivalent to the norm (1) i.e. 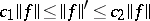 , where
, where 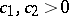 do not depend on
do not depend on  . When
. When 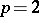 , (1prm) is a Hilbert norm, and this fact is widely used in applications.
, (1prm) is a Hilbert norm, and this fact is widely used in applications.
The boundary 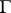 of a bounded domain
of a bounded domain  is said to be Lipschitz if for any
is said to be Lipschitz if for any 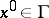 there is a rectangular coordinate system
there is a rectangular coordinate system 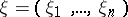 with origin
with origin 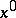 so that the box
so that the box
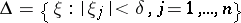 |
is such that the intersection 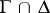 is described by a function
is described by a function 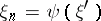 , with
, with
 |
which satisfies on 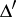 (the projection of
(the projection of 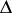 onto the plane
onto the plane 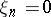 ) the Lipschitz condition
) the Lipschitz condition
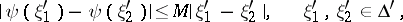 |
where the constant 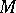 does not depend on the points
does not depend on the points 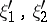 , and
, and  . All smooth and many piecewise-smooth boundaries are Lipschitz boundaries.
. All smooth and many piecewise-smooth boundaries are Lipschitz boundaries.
For a domain with a Lipschitz boundary, (1) is equivalent to the following:
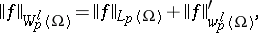 |
where
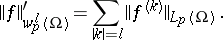 |
One can consider more general anisotropic spaces (classes) 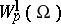 , where
, where 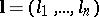 is a positive vector (see Imbedding theorems). For every such vector
is a positive vector (see Imbedding theorems). For every such vector  one can define, effectively and to a known extent exhaustively, a class of domains
one can define, effectively and to a known extent exhaustively, a class of domains 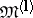 with the property that if
with the property that if 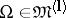 , then any function
, then any function 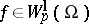 can be extended to
can be extended to 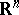 within the same class. More precisely, it is possible to define a function
within the same class. More precisely, it is possible to define a function 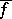 on
on 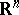 with the properties
with the properties
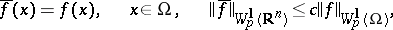 |
where  does not depend on
does not depend on 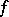 (see [3]).
(see [3]).
In virtue of this property, inequalities of the type found in imbedding theorems for functions 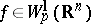 automatically carry over to functions
automatically carry over to functions 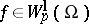 ,
, 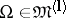 .
.
For vectors 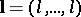 , the domains
, the domains 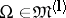 have Lipschitz boundaries, and
have Lipschitz boundaries, and 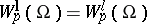 .
.
The investigation of the spaces (classes) 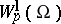 (
(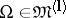 ) is based on special integral representations for functions belonging to these classes. The first such representation was obtained (see [1], [2]) for an isotropic space
) is based on special integral representations for functions belonging to these classes. The first such representation was obtained (see [1], [2]) for an isotropic space 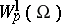 of a domain
of a domain  , star-shaped with respect to some sphere. For the further development of this method see, for example, [3].
, star-shaped with respect to some sphere. For the further development of this method see, for example, [3].
The classes 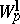 and
and 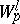 can be generalized to the case of fractional
can be generalized to the case of fractional 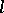 , or vectors
, or vectors 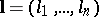 with fractional components
with fractional components 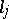 .
.
The space 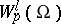 can also be defined for negative integers
can also be defined for negative integers 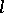 . Its elements are usually generalized functions, that is, linear functionals
. Its elements are usually generalized functions, that is, linear functionals 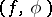 on infinitely-differentiable functions
on infinitely-differentiable functions 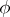 with compact support in
with compact support in  .
.
By definition, a generalized function 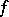 belongs to the class
belongs to the class 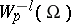 (
(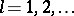 ) if
) if
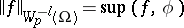 |
is finite, where the supremum is taken over all functions  with norm at most one
with norm at most one 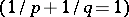 . The functions
. The functions 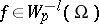 form the space adjoint to the Banach space
form the space adjoint to the Banach space 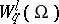 .
.
References
| [1] | S.L. Sobolev, "On a theorem of functional analysis" Transl. Amer. Math. Soc. (2) , 34 (1963) pp. 39–68 Mat. Sb. , 4 (1938) pp. 471–497 |
| [2] | S.L. Sobolev, "Some applications of functional analysis in mathematical physics" , Amer. Math. Soc. (1963) (Translated from Russian) |
| [3] | O.V. Besov, V.P. Il'in, S.M. Nikol'skii, "Integral representations of functions and imbedding theorems" , 1–2 , Wiley (1978) (Translated from Russian) |
| [4] | S.M. Nikol'skii, "Approximation of functions of several variables and imbedding theorems" , Springer (1975) (Translated from Russian) |
Comments
References
| [a1] | V.G. Maz'ja, "Sobolev spaces" , Springer (1985) |
| [a2] | F. Trèves, "Basic linear partial differential equations" , Acad. Press (1975) pp. Sects. 24–26 |
| [a3] | R.A. Adams, "Sobolev spaces" , Acad. Press (1975) |
Sobolev space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sobolev_space&oldid=17396