Sobolev inner product
Let 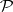 be the linear space of polynomials in one variable with real coefficients and let
be the linear space of polynomials in one variable with real coefficients and let 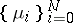 be a set of positive Borel measures supported in the real line (cf. also Borel measure; Polynomial).
be a set of positive Borel measures supported in the real line (cf. also Borel measure; Polynomial).
One introduces an inner product in 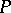
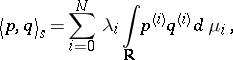 | (a1) |
such that the integrals are convergent for all 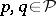 and
and 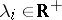 . Here,
. Here, 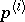 is the
is the  th derivative of
th derivative of 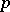 .
.
As usual, the associated norm is
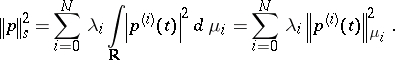 |
Inner products such as (a1) appear in least-square approximation when smooth conditions are involved both in the approximation and in the functions to be approximated. See [a4] for an introduction to this.
One says that (a1) is a Sobolev inner product in 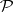 .
.
In a pioneer work, P. Althammer [a1] considered the so-called Legendre–Sobolev inner products, when 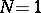 and
and 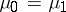 is the Lebesgue measure supported on
is the Lebesgue measure supported on 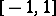 . Most of the tools of the standard case
. Most of the tools of the standard case 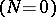 are not useful for
are not useful for 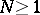 since a basic property concerning the symmetry of the shift operator is lost for (a1). This is the reason why further work focused initially on some particular cases of (a1) when
since a basic property concerning the symmetry of the shift operator is lost for (a1). This is the reason why further work focused initially on some particular cases of (a1) when 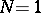 .
.
In [a6], the case 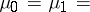 the Gegenbauer weight function and
the Gegenbauer weight function and 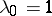 is considered with some detail. In such a situation, there exists a linear differential operator
is considered with some detail. In such a situation, there exists a linear differential operator 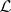 of second order such that
of second order such that 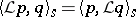 . This fact leads to the study of the algebraic properties of the so-called Gegenbauer–Sobolev orthogonal polynomials, with a special emphasis on the location of their zeros as well as their strong asymptotics (see [a10]; cf. also Orthogonal polynomials).
. This fact leads to the study of the algebraic properties of the so-called Gegenbauer–Sobolev orthogonal polynomials, with a special emphasis on the location of their zeros as well as their strong asymptotics (see [a10]; cf. also Orthogonal polynomials).
A similar approach was made in [a7] for 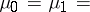 the Laguerre weight function and
the Laguerre weight function and 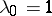 . Thus, the Laguerre–Sobolev orthogonal polynomials are introduced. Some estimates for them, as well as their relative asymptotics with respect to Laguerre polynomials off the positive real semi-axis, are given in [a8].
. Thus, the Laguerre–Sobolev orthogonal polynomials are introduced. Some estimates for them, as well as their relative asymptotics with respect to Laguerre polynomials off the positive real semi-axis, are given in [a8].
Beyond these two examples, an approach to a general theory was started in [a3], where the concept of a coherent pair of measures is introduced. The main idea consists in the assumption of a kind of correlation between the measures 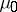 and
and 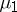 .
.
Consider an inner product
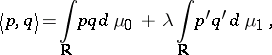 | (a2) |
with 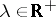 , and let
, and let 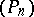 and
and 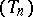 be sequences of monic polynomials orthogonal with respect to
be sequences of monic polynomials orthogonal with respect to 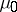 and
and 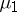 , respectively.
, respectively.
Then 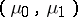 is called a
is called a 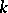 -coherent pair of measures if
-coherent pair of measures if
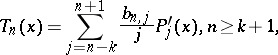 |
with 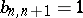 and
and  .
.
If 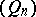 denotes the sequence of monic polynomials orthogonal with respect to (a2) and
denotes the sequence of monic polynomials orthogonal with respect to (a2) and 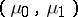 is a
is a 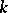 -coherent pair, then
-coherent pair, then
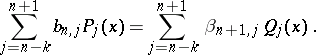 |
Thus, analytic properties of 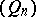 can be studied in terms of analytic properties of
can be studied in terms of analytic properties of 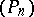 . The first problem is to classify the set of
. The first problem is to classify the set of 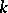 -coherent pairs of measures. This was described in [a12] for
-coherent pairs of measures. This was described in [a12] for 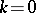 (see Table 1). Note that one of the measures must be the Jacobi or the Laguerre weight function. This means that the concept is very restrictive from the point of view of a general theory. The study of the general case
(see Table 1). Note that one of the measures must be the Jacobi or the Laguerre weight function. This means that the concept is very restrictive from the point of view of a general theory. The study of the general case 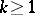 remains open (as of 2000).
remains open (as of 2000).

Figure: s130410a
Table 1
Nevertheless, in [a9] a first approach is given when 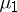 is the Jacobi weight function.
is the Jacobi weight function.
Let 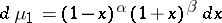 ,
, 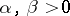 , supported on
, supported on 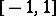 . The measure
. The measure  is said to be admissible with respect to
is said to be admissible with respect to 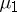 if
if
i) 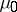 belongs to the Szegö class, i.e.,
belongs to the Szegö class, i.e.,
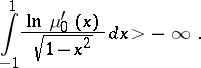 |
ii) 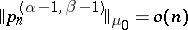 ,
, 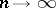 , where
, where 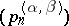 denotes the sequence of orthonormal Jacobi polynomials. In such a case one obtains the following relative asymptotics: for
denotes the sequence of orthonormal Jacobi polynomials. In such a case one obtains the following relative asymptotics: for 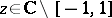 ,
,
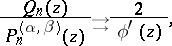 |
where 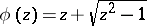 , with
, with 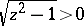 when
when 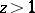 .
.
This result has been extended [a11] to the case when 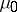 and
and 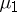 are absolutely continuous measures supported in
are absolutely continuous measures supported in 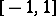 and belong to the Szegö class.
and belong to the Szegö class.
In fact, 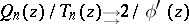 ,
, 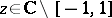 .
.
From a numerical point of view, [a2] is a nice survey about the location of zeros of polynomials orthogonal with respect to (a1) when 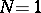 . For more information about Sobolev inner products, see the surveys [a5] and [a13].
. For more information about Sobolev inner products, see the surveys [a5] and [a13].
References
| [a1] | P. Althammer, "Eine Erweiterung des Orthogonalitätsbegriffes bei Polynomen und deren Anwendung auf die beste Approximation" J. Reine Angew. Math. , 211 (1962) pp. 192–204 |
| [a2] | W. Gautschi, M. Zhang, "Computing orthogonal polynomials in Sobolev spaces" Numer. Math. , 71 (1995) pp. 159–184 |
| [a3] | A. Iserles, P.E. Koch, S.P. Norsett, J.M. Sanz-Serna, "On polynomials orthogonal with respect to certain Sobolev inner products" J. Approx. Th. , 65 (1991) pp. 151–175 |
| [a4] | D.C. Lewis, "Polynomial least square approximations" Amer. J. Math. , 69 (1947) pp. 273–278 |
| [a5] | F. Marcellán, M. Alfaro, M.L. Rezola, "Orthogonal polynomials on Sobolev spaces: Old and new directions" J. Comput. Appl. Math. , 48 (1993) pp. 113–131 |
| [a6] | F. Marcellán, T.E. Pérez, M.A. Piñar, "Gegenbauer–Sobolev orthogonal polynomials" A. Cuyt (ed.) , Proc. Conf. Nonlinear Numerical Methods and Rational Approximation II , Kluwer Acad. Publ. (1994) pp. 71–82 |
| [a7] | F. Marcellán, T.E. Pérez, M.A. Piñar, "Laguerre–Sobolev orthogonal polynomials" J. Comput. Appl. Math. , 71 (1996) pp. 245–265 |
| [a8] | F. Marcellán, H.G. Meijer, T.E. Pérez, M.A. Piñar, "An asymptotic result for Laguerre–Sobolev orthogonal polynomials" J. Comput. Appl. Math. , 87 (1997) pp. 87–94 |
| [a9] | A. Martínez-Finkelshtein, J.J. Moreno-Balcázar, "Asymptotics of Sobolev orthogonal polynomials for a Jacobi weight" Meth. Appl. Anal. , 4 (1997) pp. 430–437 |
| [a10] | A. Martínez-Finkelshtein, J.J. Moreno-Balcázar, H. Pijeira, "Strong asymptotics for Gegenbauer–Sobolev orthogonal polynomials" J. Comput. Appl. Math. , 81 (1997) pp. 211–216 |
| [a11] | A. Martínez-Finkelshtein, "Bernstein–Szegő's theorem for Sobolev orthogonal polynomials" Constructive Approx. (2000) pp. 73–84 |
| [a12] | H.G. Meijer, "Determination of all coherent pairs of functionals" J. Approx. Th. , 89 (1997) pp. 321–343 |
| [a13] | H.G. Meijer, "A short history of orthogonal polynomials in a Sobolev space I: The non-discrete case" Nieuw Arch. Wisk. , 14 (1996) pp. 93–112 |
Sobolev inner product. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sobolev_inner_product&oldid=13233