Sine
One of the trigonometric functions:
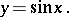 |
The domain of definition is the whole real line and the range of values is the interval 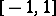 . The sine is an odd periodic function of period
. The sine is an odd periodic function of period 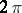 . Sine and cosine are connected by the formula
. Sine and cosine are connected by the formula
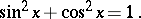 |
Sine and cosecant are connected by the formula
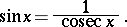 |
The derivative of sine is:
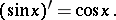 |
The indefinite integral of sine is:
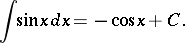 |
Sine has the following power series representation:
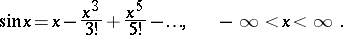 |
The function inverse to sine is called arcsine.
The sine and cosine of a complex argument  are related to the exponential function by Euler's formulas:
are related to the exponential function by Euler's formulas:
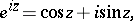 |
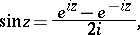 |
and if 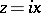 is pure imaginary, then
is pure imaginary, then
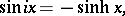 |
where 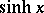 is the hyperbolic sine.
is the hyperbolic sine.
Comments
Of course, 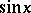 can be defined by the Euler formulas or by its power series. A visual definition runs as follows. Consider the unit circle with centre at the origin
can be defined by the Euler formulas or by its power series. A visual definition runs as follows. Consider the unit circle with centre at the origin 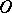 in a rectangular coordinate system and with a rotating radius vector
in a rectangular coordinate system and with a rotating radius vector 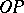 . Let
. Let  be the angle between
be the angle between 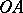 and
and 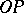 (being reckoned positive in the counter-clockwise direction) and let
(being reckoned positive in the counter-clockwise direction) and let 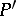 be the projection of
be the projection of 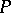 on
on 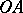 . Then
. Then 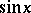 is defined as the ratio
is defined as the ratio 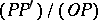 ,
, 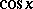 as the ratio
as the ratio 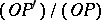 and
and 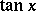 as the ratio
as the ratio 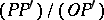 .
.
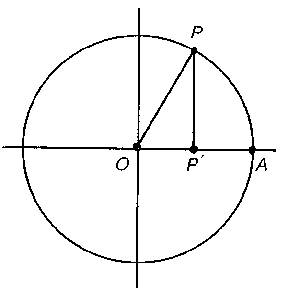
Figure: s085480a
Another, analytical, approach starts with the function 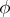 defined on the closed interval
defined on the closed interval 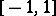 by
by 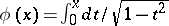 . For
. For  this integral is improper, but convergent. It is easy to see that
this integral is improper, but convergent. It is easy to see that  is monotone increasing and continuous on the closed interval
is monotone increasing and continuous on the closed interval 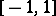 and differentiable on the open interval
and differentiable on the open interval 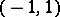 , and has values in
, and has values in 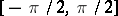 . So it has an inverse function, defined on
. So it has an inverse function, defined on 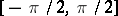 , with values in
, with values in 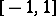 . This function is called
. This function is called 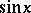 , and it can be proved that the domain of definition of this function can be continued to the whole real axis. The function
, and it can be proved that the domain of definition of this function can be continued to the whole real axis. The function 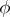 is called arcsine.
is called arcsine.
The graph of 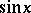 is the sinusoid (see also Trigonometric functions).
is the sinusoid (see also Trigonometric functions).
References
| [a1] | M. Abramowitz, I.A. Stegun, "Handbook of mathematical functions" , Dover, reprint (1972) pp. §4.3 |
Sine. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sine&oldid=19310