Shirshov basis
Širšov basis
A particular basis for free Lie algebras introduced in [a1]. It is identical, up to symmetries, to the Lyndon basis (cf Lyndon word; Lie algebra, free).
A word is a sequence of letters  , that is, elements chosen from a set
, that is, elements chosen from a set  called an alphabet. A word is usually written as
called an alphabet. A word is usually written as 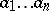 , or abbreviated by a single symbol:
, or abbreviated by a single symbol: 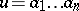 . The length of
. The length of 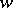 is equal to the number of letters in
is equal to the number of letters in  , i.e.
, i.e.  . One may concatenate words
. One may concatenate words 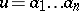 ,
,  and this operation is concisely written as
and this operation is concisely written as 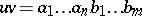 . The set of all words over
. The set of all words over 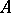 is denoted by
is denoted by 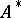 .
.
Shirshov's original description, as given in [a2], is as follows. Let 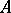 be a set totally ordered by a relation
be a set totally ordered by a relation 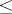 (cf. Totally ordered set). Extend the order to all words by setting
(cf. Totally ordered set). Extend the order to all words by setting 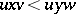 and
and 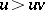 for all
for all 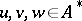 and
and 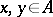 such that
such that 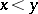 .
.
Let 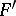 be the set of words
be the set of words 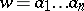 strictly greater, with respect to
strictly greater, with respect to 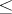 , than any of their circular shifts
, than any of their circular shifts 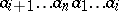 (
(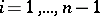 ). Shirshov's lemma [a1] shows that any word
). Shirshov's lemma [a1] shows that any word  is a non-decreasing product of words in
is a non-decreasing product of words in  :
: 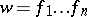 with
with 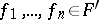 and
and 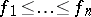 . As for Lyndon words (cf. Lyndon word), words in
. As for Lyndon words (cf. Lyndon word), words in 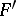 lead to a basis of the free Lie algebra (over
lead to a basis of the free Lie algebra (over 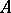 ; cf. Lie algebra, free). Indeed, only a bracketing
; cf. Lie algebra, free). Indeed, only a bracketing  of words in
of words in 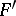 is needed. This is done inductively as follows. Set
is needed. This is done inductively as follows. Set 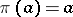 for
for 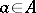 . Otherwise, a
. Otherwise, a 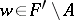 may be written as
may be written as 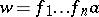 with
with  ,
, 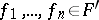 and
and 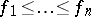 . Then one defines
. Then one defines
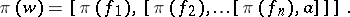 |
The set 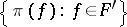 is the Shirshov basis for the free Lie algebra over
is the Shirshov basis for the free Lie algebra over 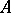 .
.
References
| [a1] | A.I. Shirshov, "On bases for free Lie algebras" Algebra i Logika Sém. , 1 (1962) pp. 14–19 (In Russian) |
| [a2] | X. Viennot, "Algèbres de Lie libres et monoïdes libres" , Lecture Notes in Mathematics , 691 , Springer (1978) |
Shirshov basis. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Shirshov_basis&oldid=11952