Sequence category
category of sequences
A particular case of the general construction of functor categories or diagram categories. Let  be the set of integers equipped with the usual order relation. Then
be the set of integers equipped with the usual order relation. Then  can be considered as a small category with integers as objects and all possible pairs
can be considered as a small category with integers as objects and all possible pairs  , where
, where  and
and  , as morphisms. The pair
, as morphisms. The pair  is the unique morphism from the object
is the unique morphism from the object  to the object
to the object  . Composition of morphisms is defined as follows:
. Composition of morphisms is defined as follows:  .
.
For an arbitrary category 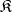 , the category of functors from
, the category of functors from 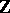 to
to 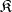 is called the category of sequences in
is called the category of sequences in 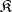 . To define a functor
. To define a functor 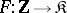 , it is sufficient to indicate a family of objects from
, it is sufficient to indicate a family of objects from 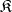 , indexed by the integers, and for each integer
, indexed by the integers, and for each integer 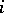 to choose a morphism
to choose a morphism 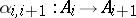 . Then the assignment
. Then the assignment 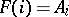 ,
, 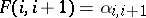 extends uniquely to a functor
extends uniquely to a functor 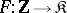 . A natural transformation
. A natural transformation 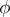 from the functor
from the functor  to a functor
to a functor 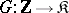 , i.e. a morphism in the category of sequences, is defined by a family of morphisms
, i.e. a morphism in the category of sequences, is defined by a family of morphisms  such that
such that 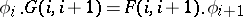 for any
for any 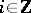 .
.
If 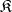 is a category with null morphisms, then in the category of sequences in
is a category with null morphisms, then in the category of sequences in 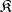 one can isolate the full subcategory of complexes, i.e. functors
one can isolate the full subcategory of complexes, i.e. functors 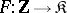 such that
such that 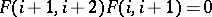 for any
for any 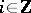 . For any Abelian category
. For any Abelian category 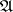 the category of sequences and the subcategory of complexes are Abelian categories.
the category of sequences and the subcategory of complexes are Abelian categories.
Instead of the category 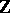 one can consider its subcategories of non-negative or non-positive numbers. The corresponding diagram categories are also called categories of sequences.
one can consider its subcategories of non-negative or non-positive numbers. The corresponding diagram categories are also called categories of sequences.
Comments
References
| [a1] | S. MacLane, "Homology" , Springer (1963) pp. Chapt. IX, §3 |
Sequence category. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sequence_category&oldid=17892