Separation axiom
A condition imposed on a topological space, expressing the requirement that some disjoint (i.e. not having common points) sets can be topologically separated from each other in a specific way. The simplest (i.e. weakest) of these axioms apply only to one-point sets, i.e. to the points of a space. These are the so-called axioms  (Kolmogorov's separation axiom, cf. also Kolmogorov space; Kolmogorov axiom) and
(Kolmogorov's separation axiom, cf. also Kolmogorov space; Kolmogorov axiom) and  . The next in line are
. The next in line are  (Hausdorff's separation axiom),
(Hausdorff's separation axiom), 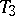 (regularity axiom) and
(regularity axiom) and  (normality axiom), which require, respectively, that every two different points (axiom
(normality axiom), which require, respectively, that every two different points (axiom  ), every point and every closed set not containing it (axiom
), every point and every closed set not containing it (axiom  ), and every two disjoint closed sets (axiom
), and every two disjoint closed sets (axiom 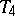 ) can be separated by neighbourhoods, i.e. are contained in disjoint open sets of the given space.
) can be separated by neighbourhoods, i.e. are contained in disjoint open sets of the given space.
A topological space which satisfies the axiom 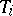 ,
, 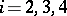 , is called a
, is called a 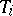 -space; a
-space; a 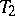 -space is also called a Hausdorff space (cf. Hausdorff space), and a
-space is also called a Hausdorff space (cf. Hausdorff space), and a 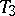 -space is called regular (cf. Regular space); a Hausdorff
-space is called regular (cf. Regular space); a Hausdorff 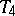 -space is always regular and is called normal (cf. Normal space).
-space is always regular and is called normal (cf. Normal space).
Functional separation is of particular significance. Two sets 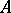 and
and 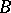 in a given topological space
in a given topological space 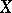 are said to be functionally separated in
are said to be functionally separated in 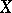 if there exists a real-valued bounded continuous function
if there exists a real-valued bounded continuous function 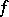 , defined throughout the space, which takes one value
, defined throughout the space, which takes one value  at all points of the set
at all points of the set 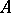 , and a value
, and a value 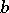 , different from
, different from  , at all points of the set
, at all points of the set 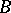 . It can always be supposed that
. It can always be supposed that 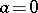 ,
,  , and that
, and that 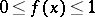 at all points
at all points  .
.
Two functionally-separable sets are always separable by neighbourhoods, but the converse is not always true. However, Urysohn's lemma holds: In a normal space, every two disjoint closed sets are functionally separable. A space in which every point is functionally separable from every closed set not containing it is called completely regular (cf. Completely regular space). A completely regular 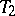 -space is called a Tikhonov space.
-space is called a Tikhonov space.
References
| [1] | P.S. Aleksandrov, "Einführung in die Mengenlehre und die allgemeine Topologie" , Deutsch. Verlag Wissenschaft. (1984) (Translated from Russian) |
Comments
The reader is warned that there is not really one convention here. There are authors who equate 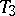 and regularity, and
and regularity, and 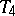 and normality and take both to include the
and normality and take both to include the 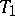 -property, e.g., [a1].
-property, e.g., [a1].
In [a2] one finds the convention that "T3=regular+T1" and "T4=normal+T1" , where [a3] adopts "regular=T3+T1" and "normal=T4+T1" .
The standpoint of [a1] seems to be the most widely accepted.
The adjective "completely regular" is often associated with the letter  .
.
References
| [a1] | R. Engelking, "General topology" , Heldermann (1989) |
| [a2] | J.L. Kelley, "General topology" , Springer (1975) |
| [a3] | B. von Querenburg, "Mengentheoretische Topologie" , Springer (1973) |
Separation axiom. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Separation_axiom&oldid=17073