Semi-simple endomorphism
semi-simple linear transformation, of a vector space  over a field
over a field 
An endomorphism  of
of  with the following property: For any
with the following property: For any  -invariant subspace
-invariant subspace  of
of  there exists an
there exists an 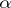 -invariant subspace
-invariant subspace  such that
such that 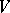 is the direct sum of
is the direct sum of 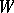 and
and 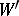 . In other words,
. In other words, 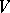 should be a semi-simple module over the ring
should be a semi-simple module over the ring 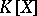 ,
,  acting as
acting as 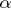 . For example, any orthogonal, symmetric or skew-symmetric linear transformation of a finite-dimensional Euclidean space, and also any diagonalizable (i.e. representable by a diagonal matrix with respect to some basis) linear transformation of a finite-dimensional vector space, is a semi-simple endomorphism. The semi-simplicity of an endomorphism is preserved by passage to an invariant subspace
. For example, any orthogonal, symmetric or skew-symmetric linear transformation of a finite-dimensional Euclidean space, and also any diagonalizable (i.e. representable by a diagonal matrix with respect to some basis) linear transformation of a finite-dimensional vector space, is a semi-simple endomorphism. The semi-simplicity of an endomorphism is preserved by passage to an invariant subspace 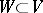 , and to the quotient space
, and to the quotient space 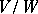 .
.
Let  . An endomorphism
. An endomorphism 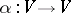 is semi-simple if and only if its minimum polynomial (cf. Matrix) has no multiple factors. Let
is semi-simple if and only if its minimum polynomial (cf. Matrix) has no multiple factors. Let  be an extension of the field
be an extension of the field 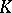 and let
and let  be the extension of the endomorphism
be the extension of the endomorphism 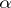 to the space
to the space 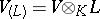 . If
. If 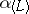 is semi-simple, then
is semi-simple, then 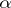 is also semi-simple, and if
is also semi-simple, and if 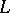 is separable over
is separable over 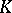 , then the converse is true. An endomorphism
, then the converse is true. An endomorphism 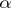 is called absolutely semi-simple if
is called absolutely semi-simple if 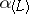 is semi-simple for any extension
is semi-simple for any extension 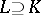 ; for this it is necessary and sufficient that the minimum polynomial has no multiple roots in the algebraic closure
; for this it is necessary and sufficient that the minimum polynomial has no multiple roots in the algebraic closure 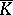 of
of 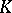 , that is, that the endomorphism
, that is, that the endomorphism 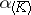 is diagonalizable.
is diagonalizable.
References
| [1] | N. Bourbaki, "Algèbre" , Eléments de mathématiques , Hermann (1970) pp. Chapts. I-III |
Comments
Over an algebraically closed field any endomorphism  of a finite-dimensional vector space can be decomposed into a sum
of a finite-dimensional vector space can be decomposed into a sum  of a semi-simple endomorphism
of a semi-simple endomorphism  and a nilpotent one
and a nilpotent one  such that
such that  ; cf. Jordan decomposition, 2).
; cf. Jordan decomposition, 2).
Semi-simple endomorphism. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Semi-simple_endomorphism&oldid=16870