Semi-lattice
A commutative idempotent semi-group, that is, a semi-group satisfying the identities 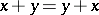 and
and 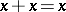 . Every semi-lattice
. Every semi-lattice 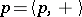 can be turned into a partially ordered set (the partial order
can be turned into a partially ordered set (the partial order 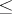 is defined by the relation
is defined by the relation 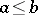 if and only if
if and only if  ) in which for any pair of elements there is a least upper bound
) in which for any pair of elements there is a least upper bound 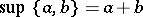 . Conversely, every partially ordered set with least upper bounds for every pair of elements is a semi-lattice with respect to the operation
. Conversely, every partially ordered set with least upper bounds for every pair of elements is a semi-lattice with respect to the operation 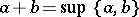 . In this case one says that the partially ordered set is an upper semi-lattice (or a join semi-lattice, or a
. In this case one says that the partially ordered set is an upper semi-lattice (or a join semi-lattice, or a  -semi-lattice). A lower semi-lattice, also called a meet semi-lattice or a
-semi-lattice). A lower semi-lattice, also called a meet semi-lattice or a 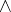 -semi-lattice, is dually defined as a partially ordered set in which any two elements have a greatest lower bound.
-semi-lattice, is dually defined as a partially ordered set in which any two elements have a greatest lower bound.
Comments
A band is a semi-group every element of which is idempotent (cf. also Band of semi-groups) (which is a decomposition of a semi-group into sub-semi-groups forming a band). Thus, an upper (lower) semi-lattice defines a commutative band, and conversely.
References
| [a1] | A.H. Clifford, G.B. Preston, "The algebraic theory of semigroups" , 1 , Amer. Math. Soc. (1961) pp. §1.8 |
Semi-lattice. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Semi-lattice&oldid=18518