Difference between revisions of "Self-injective ring"
(Importing text file) |
m (link) |
||
| Line 1: | Line 1: | ||
''left'' | ''left'' | ||
| − | A ring that, as a left module over itself, is injective (cf. [[Injective module|Injective module]]). A right self-injective ring is defined in a symmetric way. The classical semi-simple rings and all rings of residues of integers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083900/s0839001.png" /> are self-injective rings. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083900/s0839002.png" /> is a self-injective ring with [[Jacobson radical|Jacobson radical]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083900/s0839003.png" />, then the quotient ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083900/s0839004.png" /> is a [[Regular ring (in the sense of von Neumann)|regular ring (in the sense of von Neumann)]]. A regular self-injective ring is continuous. Every countable self-injective ring is quasi-Frobenius (cf. [[Quasi-Frobenius ring|Quasi-Frobenius ring]]). A left self-injective ring is not necessarily right self-injective. The ring of matrices over a self-injective ring and the complete ring of linear transformations of a vector space over a field are self-injective. The rings of endomorphisms of all free left <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083900/s0839005.png" />-modules are self-injective rings if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083900/s0839006.png" /> is quasi-Frobenius. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083900/s0839007.png" /> is the cogenerator of the category of left <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083900/s0839008.png" />-modules, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083900/s0839009.png" /> is a self-injective ring. If the singular ideal of a ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083900/s08390010.png" /> is zero, then its injective hull can be made into a self-injective ring in a natural way. A group ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083900/s08390011.png" /> is left self-injective if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083900/s08390012.png" /> is a self-injective ring and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083900/s08390013.png" /> is a finite group. The direct product of self-injective rings is self-injective. A ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083900/s08390014.png" /> is isomorphic to the direct product of complete rings of linear transformations over fields if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083900/s08390015.png" /> is a left self-injective ring without nilpotent ideals for which every non-zero left ideal contains a minimal left ideal. | + | A ring that, as a left module over itself, is injective (cf. [[Injective module|Injective module]]). A right self-injective ring is defined in a symmetric way. The classical semi-simple rings and all rings of residues of integers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083900/s0839001.png" /> are self-injective rings. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083900/s0839002.png" /> is a self-injective ring with [[Jacobson radical|Jacobson radical]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083900/s0839003.png" />, then the quotient ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083900/s0839004.png" /> is a [[Regular ring (in the sense of von Neumann)|regular ring (in the sense of von Neumann)]]. A regular self-injective ring is continuous. Every countable self-injective ring is quasi-Frobenius (cf. [[Quasi-Frobenius ring|Quasi-Frobenius ring]]). A left self-injective ring is not necessarily right self-injective. The ring of matrices over a self-injective ring and the complete ring of linear transformations of a vector space over a field are self-injective. The rings of endomorphisms of all free left <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083900/s0839005.png" />-modules are self-injective rings if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083900/s0839006.png" /> is quasi-Frobenius. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083900/s0839007.png" /> is the cogenerator of the category of left <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083900/s0839008.png" />-modules, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083900/s0839009.png" /> is a self-injective ring. If the singular ideal of a ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083900/s08390010.png" /> is zero, then its [[injective hull]] can be made into a self-injective ring in a natural way. A group ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083900/s08390011.png" /> is left self-injective if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083900/s08390012.png" /> is a self-injective ring and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083900/s08390013.png" /> is a finite group. The direct product of self-injective rings is self-injective. A ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083900/s08390014.png" /> is isomorphic to the direct product of complete rings of linear transformations over fields if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s083/s083900/s08390015.png" /> is a left self-injective ring without nilpotent ideals for which every non-zero left ideal contains a minimal left ideal. |
====References==== | ====References==== | ||
Revision as of 20:27, 30 October 2016
left
A ring that, as a left module over itself, is injective (cf. Injective module). A right self-injective ring is defined in a symmetric way. The classical semi-simple rings and all rings of residues of integers 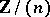 are self-injective rings. If
are self-injective rings. If 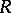 is a self-injective ring with Jacobson radical
is a self-injective ring with Jacobson radical 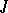 , then the quotient ring
, then the quotient ring 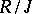 is a regular ring (in the sense of von Neumann). A regular self-injective ring is continuous. Every countable self-injective ring is quasi-Frobenius (cf. Quasi-Frobenius ring). A left self-injective ring is not necessarily right self-injective. The ring of matrices over a self-injective ring and the complete ring of linear transformations of a vector space over a field are self-injective. The rings of endomorphisms of all free left
is a regular ring (in the sense of von Neumann). A regular self-injective ring is continuous. Every countable self-injective ring is quasi-Frobenius (cf. Quasi-Frobenius ring). A left self-injective ring is not necessarily right self-injective. The ring of matrices over a self-injective ring and the complete ring of linear transformations of a vector space over a field are self-injective. The rings of endomorphisms of all free left 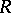 -modules are self-injective rings if and only if
-modules are self-injective rings if and only if 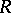 is quasi-Frobenius. If
is quasi-Frobenius. If 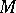 is the cogenerator of the category of left
is the cogenerator of the category of left 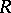 -modules, then
-modules, then 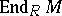 is a self-injective ring. If the singular ideal of a ring
is a self-injective ring. If the singular ideal of a ring 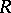 is zero, then its injective hull can be made into a self-injective ring in a natural way. A group ring
is zero, then its injective hull can be made into a self-injective ring in a natural way. A group ring 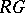 is left self-injective if and only if
is left self-injective if and only if 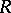 is a self-injective ring and
is a self-injective ring and 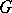 is a finite group. The direct product of self-injective rings is self-injective. A ring
is a finite group. The direct product of self-injective rings is self-injective. A ring 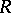 is isomorphic to the direct product of complete rings of linear transformations over fields if and only if
is isomorphic to the direct product of complete rings of linear transformations over fields if and only if 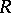 is a left self-injective ring without nilpotent ideals for which every non-zero left ideal contains a minimal left ideal.
is a left self-injective ring without nilpotent ideals for which every non-zero left ideal contains a minimal left ideal.
References
| [1] | L.A. Skornyaka, A.V. Mikhalev, "Modules" Itogi Nauk. i Tekhn. Algebra. Topol. Geom. , 14 (1976) pp. 57–190 (In Russian) |
| [2] | C. Faith, "Algebra" , 1–2 , Springer (1973–1976) |
| [3] | J. Lawrence, "A countable self-injective ring is quasi-Frobenius" Proc. Amer. Math. Soc. , 65 : 2 (1977) pp. 217–220 |
Comments
An essential right ideal of a ring 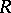 is an ideal
is an ideal 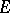 such that
such that 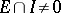 for all non-zero right ideals
for all non-zero right ideals 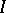 of
of 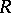 . In a right Ore domain (cf. below) every non-zero right ideal is essential. Let
. In a right Ore domain (cf. below) every non-zero right ideal is essential. Let 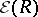 be the set of essential right ideals of
be the set of essential right ideals of 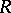 ;
;
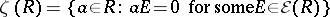 |
is an ideal, called the right singular ideal of 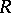 .
.
Let 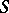 be the multiplicatively closed subset of regular elements of
be the multiplicatively closed subset of regular elements of 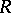 (i.e. non-zero-divisors of
(i.e. non-zero-divisors of 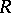 ). If
). If 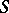 satisfies the right Ore condition (cf. Associative rings and algebras),
satisfies the right Ore condition (cf. Associative rings and algebras), 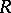 is called a right Ore ring. A right Ore domain is an integral domain that is a right Ore ring.
is called a right Ore ring. A right Ore domain is an integral domain that is a right Ore ring.
References
| [a1] | J.C. McConnell, J.C. Robson, "Noncommutative Noetherian rings" , Wiley (1987) pp. Part I, Chapt. 2 |
Self-injective ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Self-injective_ring&oldid=39562