Selberg conjecture
Let  denote the upper half-plane,
denote the upper half-plane,  the group of integer matrices of determinant one and
the group of integer matrices of determinant one and
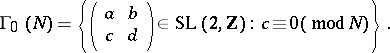 |
Following H. Maass [a9], let  denote the space of bounded functions
denote the space of bounded functions  on
on  that satisfy
that satisfy
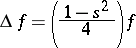 |
for
 |
the Laplace–Beltrami operator (cf. also Laplace operator). Such eigenfunctions  are called Maass wave forms. Since
are called Maass wave forms. Since 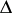 in this context is essentially self-adjoint and non-negative (cf. also Self-adjoint operator), it follows that
in this context is essentially self-adjoint and non-negative (cf. also Self-adjoint operator), it follows that 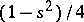 is real and
is real and  .
.
A. Selberg conjectured [a12] that there is a lower bound 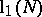 for the smallest (non-zero) eigenvalue: For
for the smallest (non-zero) eigenvalue: For 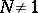 ,
,
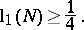 |
This innocent looking conjecture is (cf. [a10]) one of the fundamental unsolved questions in the theory of modular forms (as of 2000; cf. also Modular form). For  and for small values of
and for small values of  , it has been known for some time (Selberg, W. Roelcke). In general, it has many applications to classical number theory (see [a4] and [a12], for example). To back up his conjecture, Selberg also proved the following assertion:
, it has been known for some time (Selberg, W. Roelcke). In general, it has many applications to classical number theory (see [a4] and [a12], for example). To back up his conjecture, Selberg also proved the following assertion:
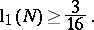 |
Selberg's approach was to relate this problem to a purely arithmetical question about certain sums of exponentials, called Kloosterman sums (cf. also Exponential sum estimates; Trigonometric sum). This allowed him to invoke results from arithmetic geometry. The key ingredient giving the estimate is a (sharp) bound on Kloosterman sums due to A. Weil [a13]. This bound, in turn, is a consequence of the Riemann hypothesis for the zeta-function of a curve over a finite field, which he had proven earlier (cf. also Riemann hypotheses). On the other hand, to go further than the theorem by this approach one needs to detect cancellations in sums of such Kloosterman sums, and arithmetic geometry offers nothing in this direction. This is the reason that the approach through Kloosterman sums has a natural barrier at  . It is interesting that H. Iwaniec [a5] has given a proof of Selberg's theorem which, while still being along the lines of Kloosterman sums, avoids appealing to Weil's bounds.
. It is interesting that H. Iwaniec [a5] has given a proof of Selberg's theorem which, while still being along the lines of Kloosterman sums, avoids appealing to Weil's bounds.
Presently (2000), Selberg's conjecture is part of the "Ramanujan–Petersson conjecture at infinity" . In other words, if interpreting the Ramanujan–Petersson conjecture as a statement about the irreducible representations of 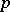 -adic groups
-adic groups 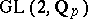 inside a cuspidal representation of
inside a cuspidal representation of 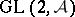 (see below), Selberg's conjecture will follow as a statement for
(see below), Selberg's conjecture will follow as a statement for 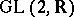 .
.
Indeed, first let 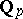 denote the completion of the rational field
denote the completion of the rational field 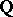 with respect to the
with respect to the 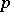 -adic absolute value
-adic absolute value  ,
, 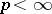 , and view
, and view 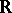 as the completion with respect to
as the completion with respect to  . By the adèles, denoted
. By the adèles, denoted 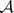 , one means the "restricted" direct product
, one means the "restricted" direct product 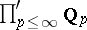 (restricted so that almost every
(restricted so that almost every  has
has  , i.e.,
, i.e., 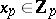 ; cf. also Adèle). Secondly, let
; cf. also Adèle). Secondly, let 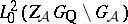 denote the space of measurable functions
denote the space of measurable functions  on
on 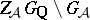 , where
, where  ( "restricted" means
( "restricted" means 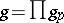 , with
, with 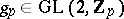 for almost every
for almost every  ),
),  imbedded diagonally in
imbedded diagonally in 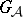 ,
,
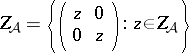 |
is the centre of  ,
,
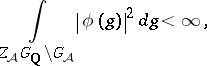 |
and
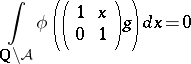 |
for almost every  . Now, assuming
. Now, assuming  is an eigenfunction of all Hecke operators
is an eigenfunction of all Hecke operators  , one can define, in a one-to-one way, a function
, one can define, in a one-to-one way, a function 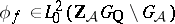 such that the
such that the  -module
-module 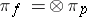 generated by the right
generated by the right 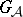 -translates of
-translates of 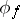 is an irreducible subrepresentation of
is an irreducible subrepresentation of 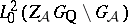 . Then Selberg's conjecture states that the representation
. Then Selberg's conjecture states that the representation 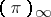 of
of 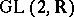 is a principal series
is a principal series  with trivial central character and
with trivial central character and
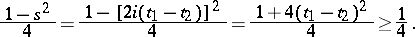 |
In other words, complementary series 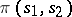 with
with  between
between  and
and 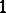 (and
(and  between
between  and
and 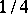 ) should not occur (cf. [a2]; see also Irreducible representation; Principal series). In this context the Ramanujan–Petersson conjecture says that for (almost every)
) should not occur (cf. [a2]; see also Irreducible representation; Principal series). In this context the Ramanujan–Petersson conjecture says that for (almost every)  the same conclusion holds, i.e., for
the same conclusion holds, i.e., for 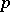 a class-one representation, that is,
a class-one representation, that is, 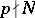 ,
,  satisfies (cf. [a11])
satisfies (cf. [a11])
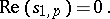 | (a1) |
P. Deligne proved the original Ramanujan conjecture [a1] when  is a holomorphic discrete series of weight
is a holomorphic discrete series of weight 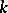 . For example, when
. For example, when 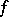 equals Ramanujan's
equals Ramanujan's 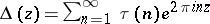 , the condition (a1) implies
, the condition (a1) implies
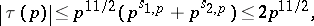 |
the famous Ramanujan inequality. In general, Deligne was able to exploit algebraic-geometric interpretations of the classical Ramanujan–Petersson identities. Note that for Selberg's conjecture one again assumes that 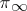 is of class-one and
is of class-one and 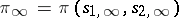 with
with
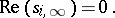 |
It was with this modern representation-theoretic point of view that progress was made on Selberg's theorem.
First, consider the mapping
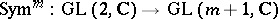 |
defined by action of 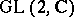 on symmetric tensors of rank
on symmetric tensors of rank 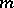 . It was conjectured by R.P. Langlands [a8] that there should be a corresponding mapping
. It was conjectured by R.P. Langlands [a8] that there should be a corresponding mapping  that (roughly) maps cuspidal automorphic representations of
that (roughly) maps cuspidal automorphic representations of  to those "of GLm+ 1" ; moreover, whenever
to those "of GLm+ 1" ; moreover, whenever 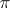 corresponds to class-one representations indexed by
corresponds to class-one representations indexed by
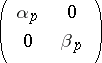 |
(including possibly 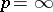 ),
), 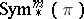 should correspond to
should correspond to 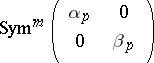 . This conjecture, for all
. This conjecture, for all 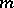 , implies both the Selberg and the Ramanujan–Petersson conjecture. In 1978, S. Gelbart and H. Jacquet [a3] proved Langlands' conjecture for
, implies both the Selberg and the Ramanujan–Petersson conjecture. In 1978, S. Gelbart and H. Jacquet [a3] proved Langlands' conjecture for  ; for Selberg's conjecture, this simply replaced the equality in his theorem by an inequality. Then, in 1994 [a7], W. Luo, Z. Rudnick and P. Sarnak used
; for Selberg's conjecture, this simply replaced the equality in his theorem by an inequality. Then, in 1994 [a7], W. Luo, Z. Rudnick and P. Sarnak used 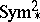 and analytic properties of
and analytic properties of  -functions to go well beyond Selberg's conjecture:
-functions to go well beyond Selberg's conjecture:
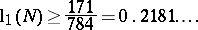 |
And in 2000, H. Kim and F. Shahidi [a6] proved Langlands' conjecture for 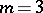 and established
and established  , i.e.,
, i.e.,
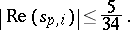 |
Either Selberg's conjecture will continue to be proved along the lines of Langlands' conjecture, or by entirely new ideas.
There is a far-reaching generalization of Selberg's conjecture to 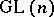 : If
: If 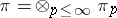 is an irreducible cuspidal automorphic representation of
is an irreducible cuspidal automorphic representation of 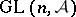 , then every class-one local representation of
, then every class-one local representation of 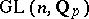 is "tempered" .
is "tempered" .
References
| [a1] | P. Deligne, "La conjecture de Weil I" Publ. Math. IHES , 43 (1974) pp. 273–307 |
| [a2] | I. Gel'fand, M. Graev, I. Piatetski-Shapiro, "Representation theory and automorphic functions" , W.B. Saunders (1969) |
| [a3] | S. Gelbart, H. Jacquet, "A relation between automorphic representations of 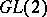 and and 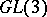 " Ann. Sci. École Norm. Sup. , 11 (1978) pp. 471–552 " Ann. Sci. École Norm. Sup. , 11 (1978) pp. 471–552 |
| [a4] | D. Hejhal, "The Selberg trace formula II" , Lecture Notes in Mathematics , 1001 , Springer (1983) |
| [a5] | H. Iwaniec, "Selberg's lower bound for the first eigenvalue of congruence groups" , Number Theory, Trace Formula, Discrete Groups , Acad. Press (1989) pp. 371–375 |
| [a6] | H. Kim, F. Shahidi, "Functorial products for 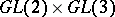 and functorial symmetric cube for and functorial symmetric cube for 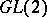 " C.R. Acad. Sci. Paris , 331 : 8 (2000) pp. 599–604 " C.R. Acad. Sci. Paris , 331 : 8 (2000) pp. 599–604 |
| [a7] | W. Luo, Z. Rudnick, P. Sarnak, "On Selberg's eigenvalue conjecture" Geom. Funct. Anal. , 5 (1995) pp. 387–401 |
| [a8] | R.P. Langlands, "Problems in the theory of automorphic forms" , Lectures in Modern Analysis and Applications , Lecture Notes in Mathematics , 170 , Springer (1970) pp. 18–86 |
| [a9] | H. Maass, "Nichtanalytishe Automorphe Funktionen" Math. Ann. , 121 (1949) pp. 141–183 |
| [a10] | P. Sarnak, "Selberg's eigenvalue conjecture" Notices Amer. Math. Soc. , 42 : 4 (1995) pp. 1272–1277 |
| [a11] | I. Satake, "Spherical functions and Ramanujan's conjecture" , Algebraic Groups and Discontinuous Subgroups , Proc. Symp. Pure Math. , IX , Amer. Math. Soc. (1966) pp. 258–264 |
| [a12] | A. Selberg, "On the estimation of Fourier coefficients of modular forms" , Proc. Symp. Pure Math. , VIII , Amer. Math. Soc. (1965) pp. 1–15 |
| [a13] | A. Weil, "On some exponential sums" Proc. Nat. Acad. Sci. , 34 (1948) pp. 204–207 |
Selberg conjecture. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Selberg_conjecture&oldid=15837