Sample method
A statistical method for the study of the general properties of a certain population of objects by studying the properties of only a sample (a part) of these objects. The mathematical theory of sample methods is based on two important sections of mathematical statistics — the theory of sampling from a finite population and the theory of sampling from an infinite population. The fundamental difference between the sampling theory for finite and infinite populations consists in the fact that in the former case the theory is usually applied to objects of a non-random, determined nature (for example, the number of defective articles in a given industrial batch of products is not a random variable: it is an unknown constant which must be estimated from the sampling data). In the latter case the theory is usually employed to study the properties of random objects (for example, to study the properties of continuously-distributed random experimental errors, each one of which may be interpreted, in principle, as the realization of one out of an infinite set of possible results).
Samples from finite populations and their theory form the base of methods in statistical quality control and are often employed in sociological studies. According to probability theory, the sample will correctly reproduce the properties of the population as a whole if the sampling is conducted at random, i.e. so that each one of the possible samples of a given size  out of a population of size
out of a population of size 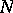 (the number of such samples is
(the number of such samples is 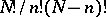 ) has an equal chance of being selected in actual practice.
) has an equal chance of being selected in actual practice.
The method which is most often used in practice is sampling without replacement, the item already chosen not being returned to the population under study before taking the next items in the sample (for example, in drawing the winning lottery tickets, in statistical quality control and in long lasting demographic investigations). Sampling with replacement is usually employed in theoretical studies only (an example of this technique is the recording of the number of particles colliding with the container walls during a given period of time in the study of Brownian motion). If 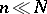 , practically equivalent results are obtained from the two techniques.
, practically equivalent results are obtained from the two techniques.
The properties of the populations which are studied by the sample method may be qualitative and quantitative. In the former case the task of investigating the sample consists of finding the number 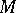 of items in the population having certain characteristics (e.g. during statistical control the parameter of interest is often the number
of items in the population having certain characteristics (e.g. during statistical control the parameter of interest is often the number 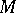 of defective items in a batch of
of defective items in a batch of 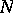 items).
items). 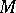 is estimated by the ratio
is estimated by the ratio 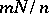 , where
, where 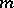 is the number of items displaying the characteristic under study in a sample of size
is the number of items displaying the characteristic under study in a sample of size  . In the case of a quantitative characteristic the task consists of determining the mean value
. In the case of a quantitative characteristic the task consists of determining the mean value 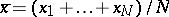 of the population. The value
of the population. The value 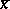 is estimated by means of the sample average
is estimated by means of the sample average
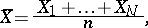 |
where 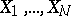 are the numbers of quantities in the populations
are the numbers of quantities in the populations 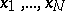 under study which belong to the sample. From the mathematical point of view, the former situation is a special case of the latter, which occurs if
under study which belong to the sample. From the mathematical point of view, the former situation is a special case of the latter, which occurs if 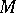 of the variables
of the variables 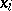 are equal to one, while the remaining
are equal to one, while the remaining 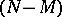 are zero; in this situation
are zero; in this situation  and
and 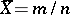 .
.
In the mathematical theory of sample methods, estimating the mean value is the key operation, since this value forms the base of a quantitative description of the variability of the characteristic within the population; in fact, the variability of the characteristic is usually defined as the variance
 |
which is the average of the squares of the deviations of 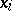 from the average value
from the average value 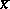 . If a qualitative characteristic is studied, then
. If a qualitative characteristic is studied, then
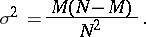 |
The accuracies of the estimates 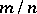 and
and 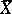 are found from their variances
are found from their variances
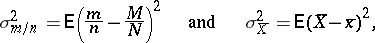 |
which are expressed, in terms of the variances 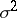 of the finite population, as the ratios
of the finite population, as the ratios 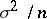 (in the case of sampling with replacement) and
(in the case of sampling with replacement) and 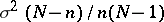 (in the case of sampling without replacement). Since in many problems of practical interest the random variables
(in the case of sampling without replacement). Since in many problems of practical interest the random variables 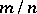 and
and 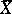 roughly follow a normal distribution if
roughly follow a normal distribution if  , it follows that the deviations of
, it follows that the deviations of 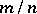 from
from 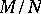 and
and 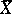 from
from  , with absolute values larger than
, with absolute values larger than 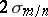 and
and 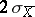 , respectively, may occur, on the average, in about one case in twenty.
, respectively, may occur, on the average, in about one case in twenty.
More complete information about the distribution of a quantitative characteristic in a given population may be obtained from the empirical distribution of this characteristic in the sample.
Sampling from an infinite population.
It is usual in mathematical statistics to describe as a sample the results of given homogeneous observations (mostly independent ones) even through this differs from the concept of a sample from a finite population with or without replacement. Thus, the measurements of angles, which involve continuously-distributed random errors, would be denoted as a sample from an infinite population. It is assumed that it is possible, in principle, to carry out any desired number of such observations. The results obtained form a so-called sample from an infinite set of possible results, which is called the general aggregate. The concept of a general aggregate is neither logically unobjectionable nor indispensable. In solving practical problems, there is no need of the infinite general aggregate itself, but only of certain characteristics corresponding to it. From the point of view of probability theory, these characteristics are numerical or functional properties of a certain probability distribution, while the sample items are random variables subject to this distribution. Such an interpretation makes it possible to apply the general theory of statistical estimation to sample estimates. This is why, for example, in probability theory, when processing observations, the concept of an infinite general aggregate is replaced by the concept of a probability distribution involving unknown parameters. The results of the observations are treated as experimentally found values of the random variables subject to this distribution. The objective of the processing is to use the results of the observations to compute optimal (in some sense) statistical estimators for the unknown distribution parameters.
So far, the concern has been with sampling from one population of certain objects. In practice, however, sampling is often performed with several identical populations (e.g. in estimating the fraction of defective articles in several batches of finished industrial products). In such a situation the object of study is no longer a single number 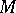 , but several unknown numbers
, but several unknown numbers 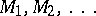 . For instance, let each batch of the finished product contain
. For instance, let each batch of the finished product contain 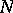 articles, let
articles, let 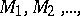 be the numbers of defective articles in these batches, and let
be the numbers of defective articles in these batches, and let 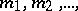 be the corresponding numbers of defective articles found in samples of size
be the corresponding numbers of defective articles found in samples of size  . If the so-called principle of defect-free acceptance is accepted, the
. If the so-called principle of defect-free acceptance is accepted, the  -th batch is delivered to the customer if
-th batch is delivered to the customer if 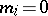 and is rejected otherwise. If it is assumed that the control of the articles involves their destruction, then the customer obtains a batch of size
and is rejected otherwise. If it is assumed that the control of the articles involves their destruction, then the customer obtains a batch of size 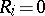 (if
(if 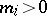 ) or a batch of size
) or a batch of size 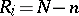 containing
containing 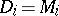 (if
(if  ) defective articles, the values of
) defective articles, the values of 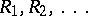 (thus, their sum as well) being known, while the value of
(thus, their sum as well) being known, while the value of 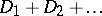 is not known. The ratio
is not known. The ratio 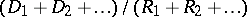 is known as the fraction of passed defectives, and its mathematical expectation
is known as the fraction of passed defectives, and its mathematical expectation 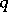 is known as the average fraction of passed defectives. The task of mathematical statistics is to estimate
is known as the average fraction of passed defectives. The task of mathematical statistics is to estimate 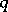 from the values of
from the values of 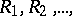 which are determined using the sample method. If the values
which are determined using the sample method. If the values 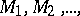 may be treated as the realization of independent identically-distributed random variables with a known distribution law
may be treated as the realization of independent identically-distributed random variables with a known distribution law 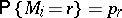 , then, according to the Bayes formula, a statistical estimator of the average number of passed defective articles in the accepted batches can be expressed by the formula
, then, according to the Bayes formula, a statistical estimator of the average number of passed defective articles in the accepted batches can be expressed by the formula
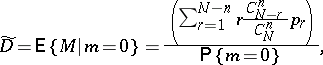 |
and
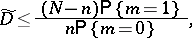 |
where
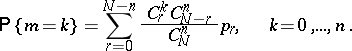 |
For this reason the estimator
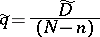 |
of the average fraction of passed defectives in the accepted batches satisfies the inequality
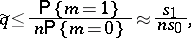 |
where 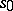 is the number of accepted batches while
is the number of accepted batches while 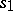 is the number of defective batches the samples of which yielded exactly one defective article.
is the number of defective batches the samples of which yielded exactly one defective article.
References
| [1] | N.V. Smirnov, I.V. Dunin-Barkovskii, "Mathematische Statistik in der Technik" , Deutsch. Verlag Wissenschaft. (1969) (Translated from Russian) |
| [2] | Yu.K. Belyaev, "Probabilistic methods of sample control" , Moscow (1975) (In Russian) |
| [3] | M.G. Kendall, A. Stuart, "The advanced theory of statistics. Distribution theory" , 3. Design and analysis , Griffin (1969) |
Comments
References
| [a1] | J.M. Juran (ed.) , Quality control handbook , McGraw-Hill (1962) |
Sample method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sample_method&oldid=16362