Sample function
sample path
A function 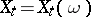 of an argument
of an argument 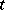 which unambiguously corresponds to each observation of a random process
which unambiguously corresponds to each observation of a random process 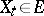 ,
, 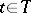 , where
, where  is a set of elementary events. The terms "realization of a random processrealization" and "trajectory of a random processtrajectory" , which are equivalent to "sample function" and "sample path" , are also frequently employed. A random process
is a set of elementary events. The terms "realization of a random processrealization" and "trajectory of a random processtrajectory" , which are equivalent to "sample function" and "sample path" , are also frequently employed. A random process 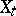 is characterized by a probability measure in the space of the sample function. In studying the local properties of the sample function
is characterized by a probability measure in the space of the sample function. In studying the local properties of the sample function 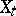 (where
(where  , and
, and  is the Euclidean space of dimension
is the Euclidean space of dimension  ) it is assumed that
) it is assumed that 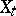 is a separable random process or that an equivalent random process with given local properties of the sample function can be found. The local properties of the sample functions of Gaussian processes (cf. Gaussian process) have been most extensively studied.
is a separable random process or that an equivalent random process with given local properties of the sample function can be found. The local properties of the sample functions of Gaussian processes (cf. Gaussian process) have been most extensively studied.
For Gaussian random processes (fields) 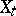 the following holds: Almost all sample functions
the following holds: Almost all sample functions 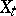 are either continuous or unbounded over some interval. For
are either continuous or unbounded over some interval. For 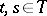 a "distance" is defined by
a "distance" is defined by 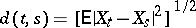 ,
, 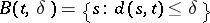 is a "ball" , and
is a "ball" , and 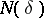 is the minimum number of such "balls" which cover
is the minimum number of such "balls" which cover 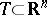 , further
, further 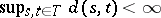 . A necessary and sufficient condition for the continuity of the sample function of a homogeneous Gaussian process has the form
. A necessary and sufficient condition for the continuity of the sample function of a homogeneous Gaussian process has the form
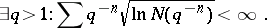 |
If
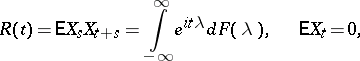 |
is concave in some neighbourhood of the point 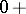 , then for the sample function
, then for the sample function 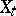 to be continuous it is necessary and sufficient that
to be continuous it is necessary and sufficient that 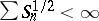 , where
, where 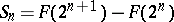 . If
. If 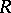 is concave in a neighbourhood of
is concave in a neighbourhood of 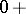 and if
and if
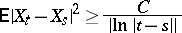 |
for 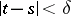 , almost all sample functions of the Gaussian random process
, almost all sample functions of the Gaussian random process 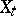 are unbounded. If
are unbounded. If
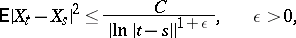 |
almost all sample functions of the Gaussian random process (field)  are continuous. For the sample function of a Gaussian random process to be continuous it is necessary and sufficient that
are continuous. For the sample function of a Gaussian random process to be continuous it is necessary and sufficient that
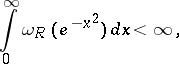 |
where  ,
,
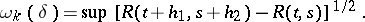 |
Here, the supremum is taken over  ,
, 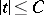 ,
, 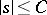 . The sample function
. The sample function 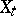 ,
, 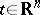 , is in the class
, is in the class 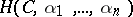 if for all sufficiently small
if for all sufficiently small 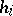 ,
,
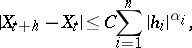 |
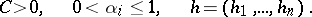 |
If 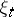 is a Gaussian random field on the unit cube
is a Gaussian random field on the unit cube 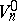 in
in 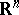 such that for sufficiently small
such that for sufficiently small 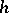 and
and  ,
,
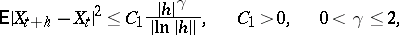 |
then, with probability one, uniformly in 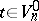 ,
,
 |
for any 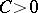 and
and 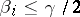 .
.
A non-decreasing continuous function 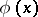 ,
, 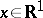 , is called an upper function if for almost all
, is called an upper function if for almost all 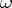 there exists an
there exists an 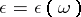 such that
such that
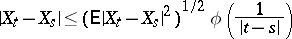 |
for 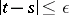 ;
; 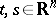 ;
; 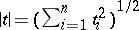 . If
. If  is a Gaussian random field with
is a Gaussian random field with
 |
then 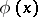 is an upper function if and only if
is an upper function if and only if
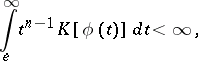 |
where
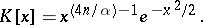 |
For almost all sample functions of a Gaussian random process to be analytic in a neighbourhood of a point 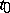 it is necessary and sufficient that the covariance function
it is necessary and sufficient that the covariance function  be analytic in
be analytic in 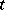 and
and  in a neighbourhood
in a neighbourhood 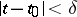 ,
, 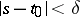 ,
, 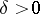 .
.
References
| [1] | J.L. Doob, "Stochastic processes" , Chapman & Hall (1953) |
| [2] | H. Cramér, M.R. Leadbetter, "Stationary and related stochastic processes" , Wiley (1967) pp. Chapts. 33–34 |
| [3] | Yu.K. Belyaev, "Continuity and Hölder's conditions for sample functions of stationary Gaussian processes" , Proc. 4-th Berkeley Symp. Math. Stat. Probab. , 2 , Univ. California Press (1961) pp. 23–33 |
| [4] | E.I. Ostrovskii, "On the local structure of Gaussian fields" Soviet Math. Dokl. , 11 : 6 (1970) pp. 1425–1427 Dokl. Akad. Nauk SSSR , 195 : 1 (1970) pp. 40–42 |
| [5] | M. Nisio, "On the continuity of stationary Gaussian processes" Nagoya Math. J. , 34 (1969) pp. 89–104 |
| [6] | R.M. Dudley, "Gaussian processes on several parameters" Ann. of Math. Statist. , 36 : 3 (1965) pp. 771–788 |
| [7] | X. Fernique, "Continuité des processus Gaussiens" C.R. Acad. Sci. Paris Sér. I Math. , 258 (1964) pp. 6058–6060 |
| [8] | M.I. Yadrenko, "Local properties of sample functions of random fields" Visnik Kiiv. Univ. Ser. Mat. Mekh. , 9 (1967) pp. 103–112 (In Ukrainian) (English abstract) |
| [9] | T. Kawada, "On the upper and lower class for Gaussian processes with several parameters" Nagoya Math. J. , 35 (1969) pp. 109–132 |
| [10] | Yu.K. Belyaev, "Analytical random processes" Theory Probab. Appl. , 4 : 4 (1959) pp. 402–409 Teor. Veroyatnost. i Primenen. , 4 : 4 (1959) pp. 437–444 |
| [11] | E.E. Slutskii, "Qualche proposizione relativa alla teoria delle funzioni aluatorie" Giorn. Inst. Ital. Attuari , 8 : 2 (1937) pp. 183–199 |
| [12] | X.M. Fernique, "Regularité de trajectoires des fonctions aleatoires gaussiennes" J.P. Conze (ed.) J. Cani (ed.) X.M. Fernique (ed.) , Ecole d'Ete de Probabilité de Saint-Flour IV-1974 , Springer (1975) pp. 1–96 |
Comments
References
| [a1] | R.J. Alder, "The geometry of random fields" , Wiley (1981) |
Sample function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sample_function&oldid=13989