Saddle point method
A method for computing the asymptotic expansion of integrals of the form
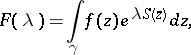 | (*) |
where  ,
,  is a large parameter,
is a large parameter,  is a contour in the complex
is a contour in the complex  -plane, and the functions
-plane, and the functions  and
and  are holomorphic in a domain
are holomorphic in a domain  containing
containing  . The zeros of
. The zeros of 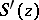 are called the saddle points of
are called the saddle points of 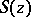 . The essence of the method is as follows. The contour
. The essence of the method is as follows. The contour 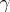 is deformed to a contour
is deformed to a contour 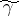 with the same end-points and lying in
with the same end-points and lying in 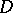 and such that
and such that 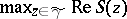 is attained only at the saddle points or at the ends of
is attained only at the saddle points or at the ends of 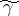 (the contour of steepest descent). The asymptotics of the integral (*) along the path of steepest descent are calculated by means of the Laplace method and are equal to the sum of the contributions from the saddle points. The contribution
(the contour of steepest descent). The asymptotics of the integral (*) along the path of steepest descent are calculated by means of the Laplace method and are equal to the sum of the contributions from the saddle points. The contribution 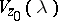 from the point
from the point 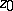 is an integral of the form of (*) taken over a small arc of
is an integral of the form of (*) taken over a small arc of 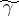 containing the point
containing the point 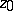 . If
. If 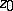 is an interior point of
is an interior point of 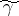 and
and 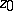 is a saddle point with
is a saddle point with 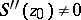 , then
, then
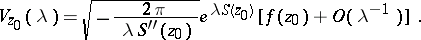 |
The contour of steepest descent has a minimax property; on it,
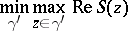 |
is attained, where the minimum is taken over all contours 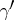 lying in
lying in 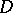 having the same end-points as
having the same end-points as  . The main difficulty in using the method is to select the saddle points, i.e. to choose the
. The main difficulty in using the method is to select the saddle points, i.e. to choose the 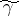 corresponding to
corresponding to 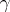 .
.
The method is due to P. Debye [1], although the ideas in the method were suggested earlier by B. Riemann [2]. See [3]–[9] for the calculation of the contributions from the saddle points and from the end-points of the contour.
The method is in essence the only method for calculating the asymptotic expansions of integrals of the form (*). It can be used to derive the asymptotic expansions for Laplace, Fourier and Mellin transforms, as well as for transforms of exponentials of polynomials and many special functions.
Let 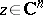 , let
, let 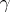 be a bounded manifold with boundary of dimension
be a bounded manifold with boundary of dimension  and of class
and of class 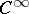 , let functions
, let functions 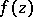 and
and 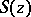 be holomorphic in a certain domain
be holomorphic in a certain domain 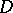 containing
containing  , and let
, and let 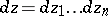 . Suppose that
. Suppose that 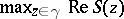 is attained at a single point
is attained at a single point 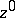 which is an interior point for
which is an interior point for 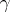 and a non-singular saddle point for
and a non-singular saddle point for 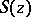 , i.e.
, i.e.  . Then the contribution from
. Then the contribution from 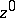 is
is
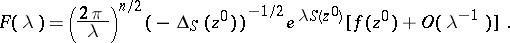 |
References
| [1] | P. Debye, "Näherungsformeln für die Zylinderfunktionen für grosse Werte des Arguments und unbeschränkt veranderliche Werte des Index" Math. Ann. , 67 (1909) pp. 535–558 |
| [2] | B. Riemann, "Mathematische Werke" , Dover, reprint (1953) |
| [3] | A. Erdélyi, "Asymptotic expansions" , Dover, reprint (1956) |
| [4] | N.G. de Bruijn, "Asymptotic methods in analysis" , Dover, reprint (1981) |
| [5] | M.A. Evgrafov, "Asymptotic estimates and entire functions" , Gordon & Breach (1962) (Translated from Russian) |
| [6] | E.T. Copson, "Asymptotic expansions" , Cambridge Univ. Press (1965) |
| [7] | F.W.J. Olver, "Asymptotics and special functions" , Acad. Press (1974) |
| [8] | E.Ya. Riekstyn'sh, "Asymptotic expansions of integrals" , 1–2 , Riga (1974–1977) (In Russian) |
| [9] | M.V. Fedoryuk, "The saddle-point method" , Moscow (1977) (In Russian) |
Comments
References
| [a1] | R. Wong, "Asymptotic approximations of integrals" , Acad. Press (1989) |
Saddle point method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Saddle_point_method&oldid=14602