Ritz method
A method for solving problems in variational calculus and, in general, finite-dimensional extremal problems, based on optimization of a functional on finite-dimensional subspaces or manifolds.
Let the problem of finding a minimum point of a functional  on a separable Banach space
on a separable Banach space  be posed, where
be posed, where  is bounded from below. Let some system of elements
is bounded from below. Let some system of elements  , complete in
, complete in  (cf. Complete system), be given (a so-called coordinate system). In the Ritz method, the minimizing element in the
(cf. Complete system), be given (a so-called coordinate system). In the Ritz method, the minimizing element in the  -th approximation is sought in the linear hull of the first
-th approximation is sought in the linear hull of the first  coordinate elements
coordinate elements  , i.e. the coefficients
, i.e. the coefficients  of the approximation
of the approximation
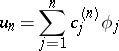 |
are defined by the condition that 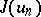 be minimal among the specified elements. Instead of a coordinate system one can specify a sequence of subspaces
be minimal among the specified elements. Instead of a coordinate system one can specify a sequence of subspaces  , not necessarily nested.
, not necessarily nested.
Let  be a Hilbert space with scalar product
be a Hilbert space with scalar product 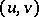 , let
, let 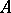 be a self-adjoint positive-definite (i.e.
be a self-adjoint positive-definite (i.e.  :
: 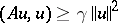 for all
for all 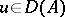 ), possibly unbounded, operator in
), possibly unbounded, operator in  , and let
, and let  be the Hilbert space obtained by completing the domain of definition
be the Hilbert space obtained by completing the domain of definition 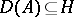 of
of 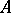 with respect to the norm
with respect to the norm  generated by the scalar product
generated by the scalar product 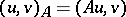 ,
,  . Let it be required to solve the problem
. Let it be required to solve the problem
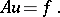 | (1) |
This is equivalent to the problem of finding a minimum point of the quadratic functional
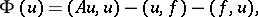 |
which can be written in the form
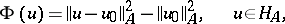 |
where  is a solution of equation (1). Let
is a solution of equation (1). Let 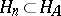 ,
, 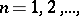 be closed (usually, finite-dimensional) subspaces such that
be closed (usually, finite-dimensional) subspaces such that 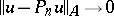 as
as  for every
for every 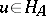 , where
, where  is the orthogonal projection in
is the orthogonal projection in  projecting onto
projecting onto  . By minimizing
. By minimizing  in
in  one obtains a Ritz approximation
one obtains a Ritz approximation 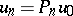 to the solution of equation (1); moreover,
to the solution of equation (1); moreover, 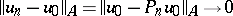 as
as  . If
. If 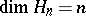 and
and  is a basis in
is a basis in  , then the coefficients of the element
, then the coefficients of the element
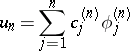 | (2) |
are determined from the linear system of equations
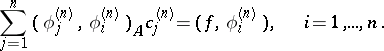 | (3) |
One can also arrive at a Ritz approximation without making use of the variational statement of the problem (1). Namely, by defining the approximation (2) from the condition
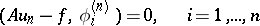 |
(the Galerkin method), one arrives at the same system of equations (3). That is why the Ritz method for equation (1) is sometimes called the Ritz–Galerkin method.
Ritz's method is widely applied when solving eigenvalue problems, boundary value problems and operator equations in general. Let 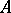 and
and  be self-adjoint operators in
be self-adjoint operators in 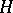 . Moreover, let
. Moreover, let 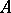 be positive definite,
be positive definite,  be positive,
be positive, 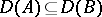 , and let the operator
, and let the operator  be completely continuous in
be completely continuous in  (cf. Completely-continuous operator). By virtue of the above requirements,
(cf. Completely-continuous operator). By virtue of the above requirements,  is self-adjoint and positive in
is self-adjoint and positive in 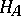 , and the spectrum of the problem
, and the spectrum of the problem
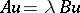 | (4) |
consists of positive eigenvalues:
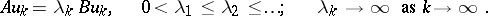 |
Ritz's method is based on a variational determination of eigenvalues. For instance,
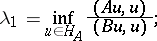 |
by carrying out minimization only over the subspace  one obtains Ritz approximations
one obtains Ritz approximations  of
of 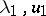 . If
. If 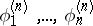 is, as above, a basis in
is, as above, a basis in 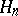 , then the Ritz approximations
, then the Ritz approximations  of
of  ,
,  , are determined from the equation
, are determined from the equation
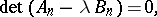 |
 |
and the vector of coefficients  of the approximation
of the approximation
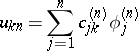 |
to 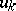 is determined as a non-trivial solution of the linear homogeneous system
is determined as a non-trivial solution of the linear homogeneous system 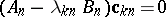 . The Ritz method provides an approximation from above of the eigenvalues, i.e.
. The Ritz method provides an approximation from above of the eigenvalues, i.e.  ,
, 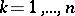 . If the
. If the  -th eigenvalue of problem (4) is simple
-th eigenvalue of problem (4) is simple 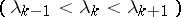 , then the convergence rate of the Ritz method is characterized by the following relations:
, then the convergence rate of the Ritz method is characterized by the following relations:
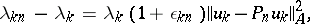 |
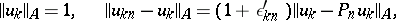 |
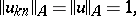 |
where 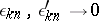 as
as  . Similar relations can be carried over to the case of multiple
. Similar relations can be carried over to the case of multiple  , but then they need certain refinements (see [2]). W. Ritz [4] proposed his method in 1908, but even earlier Lord Rayleigh had applied this method to solve certain eigenvalue problems. In this connection the Ritz method is often called the Rayleigh–Ritz method, especially if one speaks about solving an eigenvalue problem.
, but then they need certain refinements (see [2]). W. Ritz [4] proposed his method in 1908, but even earlier Lord Rayleigh had applied this method to solve certain eigenvalue problems. In this connection the Ritz method is often called the Rayleigh–Ritz method, especially if one speaks about solving an eigenvalue problem.
References
| [1] | M.M. Vainberg, "Variational method and method of monotone operators in the theory of nonlinear equations" , Wiley (1973) (Translated from Russian) |
| [2] | M.A. Krasnosel'skii, G.M. Vainikko, P.P. Zabreiko, et al., "Approximate solution of operator equations" , Wolters-Noordhoff (1972) (Translated from Russian) |
| [3] | S.G. [S.G. Mikhlin] Michlin, "Variationsmethoden der mathematischen Physik" , Akademie Verlag (1962) (Translated from Russian) |
| [4] | W. Ritz, "Ueber eine neue Methode zur Lösung gewisser Variationsprobleme der mathematischen Physik" J. Reine Angew. Math. , 135 (1908) pp. 1–61 |
Comments
References
| [a1] | G.H. Golub, C.F. van Loan, "Matrix computations" , Johns Hopkins Univ. Press (1989) |
| [a2] | G.J. Fix, "An analyse of the finite element method" , Prentice-Hall (1973) |
| [a3] | J. Stoer, R. Bulirsch, "Einführung in die numerische Mathematik" , II , Springer (1978) |
| [a4] | P.G. Ciarlet, "The finite element method for elliptic problems" , North-Holland (1975) |
Ritz method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ritz_method&oldid=19210