Riesz space
vector lattice
A real partially ordered vector space 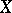 (cf. Partially ordered set; Vector space) in which
(cf. Partially ordered set; Vector space) in which
1) the vector space structure and the partial order are compatible. i.e. from 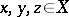 and
and 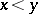 follows that
follows that 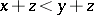 and from
and from 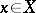 ,
, 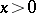 ,
, 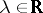 ,
, 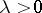 follows
follows  ;
;
2) for any two elements 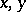 there exists
there exists 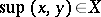 . In particular, the supremum and infimum of any finite set exist.
. In particular, the supremum and infimum of any finite set exist.
In Soviet scientific literature Riesz spaces are usually called 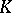 -lineals. Such spaces were first introduced by F. Riesz in 1928.
-lineals. Such spaces were first introduced by F. Riesz in 1928.
The space 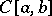 of real continuous functions with the pointwise order is an example of a Riesz space. For any element
of real continuous functions with the pointwise order is an example of a Riesz space. For any element  of a Riesz space one can define
of a Riesz space one can define 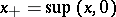 ,
, 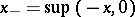 and
and 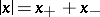 . It turns out that
. It turns out that  . In Riesz spaces one can introduce two types of convergence of a sequence
. In Riesz spaces one can introduce two types of convergence of a sequence  . Order convergence,
. Order convergence,  -convergence:
-convergence: 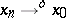 if there exist a monotone increasing sequence
if there exist a monotone increasing sequence 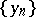 and a monotone decreasing sequence
and a monotone decreasing sequence 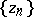 such that
such that 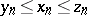 and
and  . Relative uniform convergence,
. Relative uniform convergence,  -convergence:
-convergence: 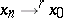 if there exists an element
if there exists an element 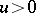 such that for any
such that for any 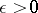 there exists an
there exists an 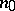 such that
such that 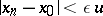 for
for 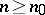 (
( -convergence is also called convergence with a regulator). The concepts of
-convergence is also called convergence with a regulator). The concepts of  - and
- and  -convergence have many of the usual properties of convergence of numerical sequences and can be naturally generalized to nets
-convergence have many of the usual properties of convergence of numerical sequences and can be naturally generalized to nets 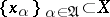 .
.
A Riesz space is called Archimedean if 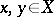 and
and 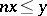 for
for 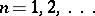 imply
imply 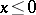 . In Archimedean Riesz spaces,
. In Archimedean Riesz spaces, 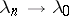 and
and 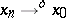 imply
imply 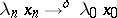 (
(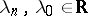 ,
, 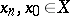 ), and
), and  -convergence implies
-convergence implies  -convergence.
-convergence.
References
| [1] | F. Riesz, "Sur la décomposition des opérations fonctionelles linéaires" , Atti congress. internaz. mathematici (Bologna, 1928) , 3 , Zanichelli (1930) pp. 143–148 |
| [2] | W.A.J. Luxemburg, A.C. Zaanen, "Riesz spaces" , I , North-Holland (1971) |
| [3] | B.Z. Vulikh, "Introduction to the theory of partially ordered spaces" , Wolters-Noordhoff (1967) (Translated from Russian) |
Comments
A Riesz subspace of a Riesz space 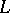 is a linear subspace
is a linear subspace 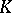 of
of 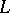 such that
such that 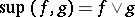 and
and 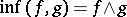 are in
are in  whenever
whenever  (where the sup and inf are those of
(where the sup and inf are those of 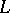 ). A subspace
). A subspace 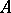 of
of 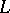 that is an order ideal, i.e.
that is an order ideal, i.e. 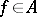 ,
, 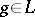 ,
, 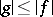 imply that
imply that 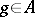 , is called a Riesz ideal. Such subspaces are called sublineals and normal sublineals in the Soviet literature. A band is a Riesz ideal
, is called a Riesz ideal. Such subspaces are called sublineals and normal sublineals in the Soviet literature. A band is a Riesz ideal 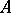 such that
such that 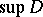 in
in 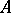 for
for  if
if 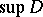 exists in
exists in 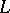 . A band is often called a component in the Soviet literature.
. A band is often called a component in the Soviet literature.
A linear operator 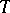 from a Riesz space
from a Riesz space 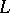 to a Riesz space
to a Riesz space 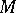 is called positive if
is called positive if  for all
for all  ,
, 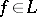 . A set
. A set 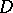 in
in  is called order bounded if there exist
is called order bounded if there exist 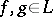 such that
such that 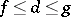 for all
for all 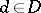 . The linear operator
. The linear operator 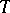 is called order bounded if it takes order-bounded sets to order-bounded sets. Taking the positive operators as the positive cone defines an order structure on the space of order-bounded operators, turning it into a Dedekind-complete Riesz space (the Freudenthal–Kantorovich theorem). Recall that a lattice is Dedekind complete if every subset bounded from below (respectively above) has an inf (respectively sup). A positive operator is order bounded, and so are differences
is called order bounded if it takes order-bounded sets to order-bounded sets. Taking the positive operators as the positive cone defines an order structure on the space of order-bounded operators, turning it into a Dedekind-complete Riesz space (the Freudenthal–Kantorovich theorem). Recall that a lattice is Dedekind complete if every subset bounded from below (respectively above) has an inf (respectively sup). A positive operator is order bounded, and so are differences 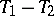 of positive operators, which are called regular operators. If
of positive operators, which are called regular operators. If 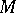 is Dedekind complete, the converse holds: Every order-bounded operator
is Dedekind complete, the converse holds: Every order-bounded operator 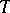 admits a Jordan decomposition
admits a Jordan decomposition 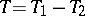 as a difference of two positive operators.
as a difference of two positive operators.
A norm  on a Riesz space
on a Riesz space 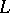 is a Riesz norm if
is a Riesz norm if 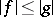 implies
implies 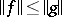 . A Riesz semi-norm is a semi-norm with the same compatibility conditions. A Riesz space with a Riesz norm is a normed Riesz space. A norm-complete normed Riesz space is a Banach lattice. An order-bounded operator
. A Riesz semi-norm is a semi-norm with the same compatibility conditions. A Riesz space with a Riesz norm is a normed Riesz space. A norm-complete normed Riesz space is a Banach lattice. An order-bounded operator 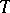 from a Banach lattice
from a Banach lattice 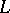 to a Dedekind-complete normed Riesz space is norm bounded.
to a Dedekind-complete normed Riesz space is norm bounded.
Let 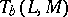 be the space of order-bounded operators from a Riesz space
be the space of order-bounded operators from a Riesz space 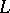 to a Dedekind-complete Riesz space
to a Dedekind-complete Riesz space 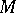 .
.  is called sequentially order continuous, or
is called sequentially order continuous, or  -order continuous, if for every sequence
-order continuous, if for every sequence 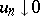 (i.e. that is monotonically decreasing to
(i.e. that is monotonically decreasing to  ) it follows that
) it follows that 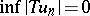 ; it is called order continuous if
; it is called order continuous if 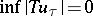 for every downwards directed system
for every downwards directed system 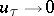 in
in 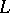 (cf. Directed set). The Soviet terminology for order-continuous and sequentially order-continuous linear operators is o-linear and (o)-linear. The order-continuous and
(cf. Directed set). The Soviet terminology for order-continuous and sequentially order-continuous linear operators is o-linear and (o)-linear. The order-continuous and  -order continuous operators are bands in
-order continuous operators are bands in 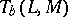 . The order dual of a Riesz space
. The order dual of a Riesz space 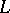 is the space of order-bounded operators of
is the space of order-bounded operators of 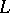 into
into 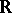 . The result that this order dual is Dedekind complete goes back to F. Riesz.
. The result that this order dual is Dedekind complete goes back to F. Riesz.
There is a second important concept of duality in Riesz space theory, reminiscent of both linear duality and the algebraic geometric duality: "ideals zero sets" , that is basic to scheme theory. It is called Baker–Benyon duality (see the volume with supplementary articles).
In the theory of linear topological spaces (cf. Topological vector space) the following criterion for boundedness of a set is used: A set B is bounded (in this theory) if and only if for every sequence 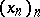 ,
, 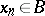 , and sequence of real numbers
, and sequence of real numbers 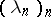 converging to zero, one has that
converging to zero, one has that 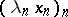 converges to zero as
converges to zero as 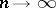 . The question arises whether order-bounded sets in a Riesz space can be characterized in this way, using instead order convergence of the
. The question arises whether order-bounded sets in a Riesz space can be characterized in this way, using instead order convergence of the  to zero. For arbitrary Dedekind-complete Riesz spaces this need not be true. The Dedekind-complete Riesz spaces for which this criterion holds are called
to zero. For arbitrary Dedekind-complete Riesz spaces this need not be true. The Dedekind-complete Riesz spaces for which this criterion holds are called  -spaces.
-spaces.
Let now 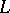 be a normed space and
be a normed space and 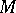 a Dedekind-complete Riesz space. A linear operator
a Dedekind-complete Riesz space. A linear operator 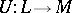 is called bo-linear if
is called bo-linear if 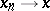 in norm implies
in norm implies  in order convergence. If
in order convergence. If 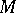 is a
is a 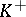 -space, then
-space, then  is bo-linear if and only if the image
is bo-linear if and only if the image 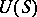 of the unit sphere
of the unit sphere 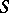 in
in 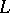 is order bounded. The element of
is order bounded. The element of 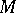 defined by
defined by
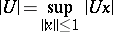 |
is then called an abstract norm for the operator  .
.
There is a variety of Riesz space analogues of Hahn–Banach type extension and existence theorems. A selection follows. Let  be a normed space,
be a normed space,  a linear subset of
a linear subset of 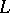 and
and  a bo-linear operator into a Dedekind-complete Riesz space
a bo-linear operator into a Dedekind-complete Riesz space 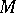 . Suppose that
. Suppose that  possesses an abstract norm. Then the operator
possesses an abstract norm. Then the operator 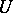 admits a bo-linear extension to all of
admits a bo-linear extension to all of 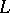 with the same abstract norm. This is one of the Kantorovich extension theorems. Another extension theorem for Riesz spaces, also due to B.Z. Kantorovich, concerns the extension of positive operators: Let
with the same abstract norm. This is one of the Kantorovich extension theorems. Another extension theorem for Riesz spaces, also due to B.Z. Kantorovich, concerns the extension of positive operators: Let 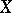 be a Riesz space and
be a Riesz space and 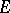 a linear subset that majorizes
a linear subset that majorizes 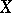 , i.e. for every
, i.e. for every 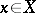 there is an
there is an 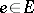 such that
such that 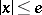 . Let
. Let 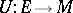 be a positive additive operator from
be a positive additive operator from 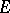 into a Dedekind-complete Riesz space
into a Dedekind-complete Riesz space 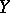 . Then there exists an additive and positive extension of
. Then there exists an additive and positive extension of  to all of
to all of 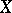 . Using these and/or related extension theorems one can show that a positive linear functional on a Riesz subspace of a Riesz space
. Using these and/or related extension theorems one can show that a positive linear functional on a Riesz subspace of a Riesz space 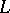 that is majorized by a Riesz semi-norm can be extended to a positive functional on all of
that is majorized by a Riesz semi-norm can be extended to a positive functional on all of  , a result which in turn serves to discuss when the order dual of
, a result which in turn serves to discuss when the order dual of 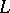 is at least non-zero.
is at least non-zero.
Examples of Riesz spaces are provided by spaces of real-valued functions on a topological space (possibly, extended real functions), where the order is defined pointwise. As in the case of, e.g., Banach algebras (cf. Banach algebra), where the Gel'fand representation provides an answer, one asks whether an arbitrary Riesz space can be seen as a space of real-valued functions on a suitable space (of ideals). The answer for Riesz spaces is given by the Yosida representation theorem and its relatives.
In the integration theory (of real functions) a basic role is played by such operations as  ,
, 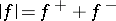 , where
, where  ,
, 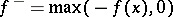 , which makes at least potentially credible that Riesz spaces might provide a suitable abstract setting for integration theory. This is indeed the case in the form of the Freudenthal spectral theorem, which will be discussed below.
, which makes at least potentially credible that Riesz spaces might provide a suitable abstract setting for integration theory. This is indeed the case in the form of the Freudenthal spectral theorem, which will be discussed below.
Let  be a lattice with zero,
be a lattice with zero,  . Let
. Let 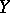 be a non-empty subset of
be a non-empty subset of 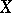 ; the set of
; the set of  that are disjoint from
that are disjoint from 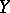 , i.e.
, i.e. 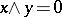 for all
for all 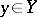 , is called the disjoint complement of
, is called the disjoint complement of 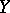 in
in 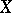 and is denoted by
and is denoted by 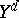 . In a Riesz space
. In a Riesz space 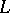 two elements
two elements  are called disjoint if
are called disjoint if 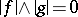 . (This agrees with the previous definition if
. (This agrees with the previous definition if 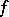 and
and 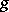 are both positive.)
are both positive.)
Given a band 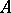 in a Riesz space
in a Riesz space 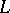 , the disjoint complement
, the disjoint complement 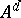 is also a band. If
is also a band. If 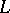 is Dedekind complete,
is Dedekind complete, 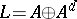 . In general, a band
. In general, a band 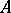 such that
such that 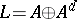 is called a projection band. A Riesz space is said to have the (principal) projection property if every (principal) band is a projection band. Thus, a Dedekind-complete Riesz space has the projection property and, a fortiori, the principal projection property.
is called a projection band. A Riesz space is said to have the (principal) projection property if every (principal) band is a projection band. Thus, a Dedekind-complete Riesz space has the projection property and, a fortiori, the principal projection property.
Let 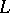 be a Riesz space with the principal projection property, let
be a Riesz space with the principal projection property, let  be a non-zero positive element of
be a non-zero positive element of 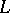 and let
and let 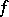 be an element in the band generated by
be an element in the band generated by  . Let
. Let  for
for 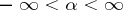 , and let
, and let 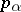 be the component of
be the component of  in the band
in the band 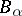 generated by
generated by 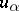 under the decomposition
under the decomposition 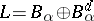 . The set
. The set 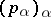 is called the spectral system of
is called the spectral system of 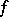 with respect to
with respect to  . Now suppose there is a finite interval such that
. Now suppose there is a finite interval such that 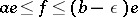 for some
for some 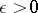 . Then
. Then 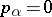 for
for 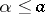 and
and 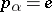 for
for 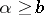 . For every partition
. For every partition 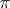 :
:  of
of 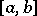 one forms the lower and upper sums
one forms the lower and upper sums
 |
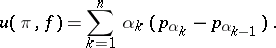 |
One then has the following result in abstract integration theory, known as the Freudenthal spectral theorem. Let 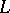 ,
,  ,
,  ,
,  ,
, 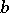 ,
,  be as above. Then
be as above. Then
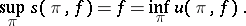 |
In the case that 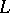 is a Riesz space of real-valued functions on a space (especially a subset of
is a Riesz space of real-valued functions on a space (especially a subset of 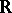 ) and
) and  , this spectral theorem expresses approximation properties of functions in
, this spectral theorem expresses approximation properties of functions in 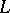 by "step functions" . The Radon–Nikodým theorem in measure theory and the Poisson formula for bounded harmonic functions on an open disc are special cases of the spectral theorem. The Freudenthal spectral theorem was one of the starting points of Riesz space theory.
by "step functions" . The Radon–Nikodým theorem in measure theory and the Poisson formula for bounded harmonic functions on an open disc are special cases of the spectral theorem. The Freudenthal spectral theorem was one of the starting points of Riesz space theory.
References
| [a1] | A.C. Zaanen, "Riesz spaces" , II , North-Holland (1983) |
| [a2] | H.H. Schaefer, "Banach lattices and positive operators" , Springer (1974) |
| [a3] | E. de Jonge, A.C.M. van Rooy, "Introduction to Riesz spaces" , Tracts , 8 , Math. Centre (1977) |
| [a4] | G. Birkhoff, "Lattice theory" , Colloq. Publ. , 25 , Amer. Math. Soc. (1973) |
| [a5] | B.Z. Kantorovich, B.Z. Vulikh, A.G. Pinsker, "Functional analysis in partially ordered spaces" , Moscow (1950) (In Russian) |
| [a6] | H. Freudenthal, "Teilweise geordneten Moduln" Proc. Royal Acad. Sci. Amsterdam , 39 (1936) pp. 641–651 |
| [a7] | H. Nakano, "Modern spectral theory" , Maruzen (1950) |
Riesz space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Riesz_space&oldid=17299