Riemann xi-function

-function

In 1859, the newly elected member of the Berlin Academy of Sciences, B.G. Riemann published an epoch-making nine-page paper [a5] (see also [a1], p. 299). In this masterpiece, Riemann's primary goal was to estimate the number of primes less than a given number (cf. also de la Vallée-Poussin theorem). Riemann considers the Euler zeta-function (also called the Riemann zeta-function or Zeta-function)

(a1)

for complex values of , where the product extends over all prime numbers and the Dirichlet series in (a1) converges for (cf. also Zeta-function). His investigation leads him to define a function, called the Riemann -function,

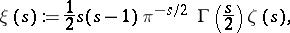(a2)

where 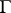denotes the gamma-function. The function is a real entire function of order one and of maximal type and satisfies the functional equation 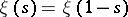[a6], p. 16. By the Hadamard factorization theorem (cf. also Hadamard theorem),

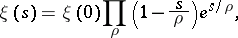where 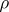ranges over the roots of the equation 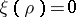. These roots (that is, the zeros of the Riemann 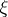-function) lie in the strip . The celebrated Riemann hypothesis (one of the most important unsolved problems in mathematics as of 2000) asserts that all the roots of 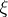lie on the critical line 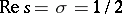(cf. [a2], [a1], [a3], [a6]; cf. also Riemann hypotheses).

The appellation "Riemann x-function" is also used in reference to the function

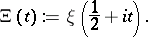(In [a5], Riemann uses the symbol 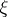to denote the function which today is denoted by 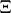.) In fact, Riemann states his conjecture in terms of the zeros of the Fourier transform [a4], p. 11,

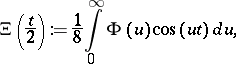where

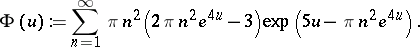The Riemann hypothesis is equivalent to the statement that all the zeros of 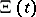are real (cf. [a6], p. 255). Indeed, Riemann writes "[…] es ist sehr wahrscheinlich, dass alle Wurzeln reell sind." (That is, it is very likely that all the roots of 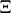are real.)

References

[a1]	H.M. Edwards, "Riemann's zeta function" , Acad. Press (1974)
[a2]	A. Ivić, "The Riemann zeta-function" , Wiley (1985)
[a3]	A.A. Karatsuba, S.M. Voronin, "The Riemann zeta-function" , de Gruyter (1992)
[a4]	G. Pólya, "Über die algebraisch-funktionentheoretischen Untersuchungen von J.L.W.V. Jensen" Kgl. Danske Vid. Sel. Math.—Fys. Medd. , 7 (1927) pp. 3–33
[a5]	B. Riemann, "Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse" Monatsber. Preuss. Akad. Wiss. (1859) pp. 671–680
[a6]	E.C. Titchmarsh, "The theory of the Riemann zeta-function" , Oxford Univ. Press (1986) ((revised by D.R. Heath–Brown))