Retract of a topological space
A subspace  of a topological space
of a topological space  for which there is a retraction of
for which there is a retraction of  onto
onto  . If
. If  is a Hausdorff space, then every retract of
is a Hausdorff space, then every retract of  is closed in
is closed in  . Every non-empty closed subset of the Cantor perfect set is a retract of it. In the transition from a space to a retract of it many important properties are preserved. In particular, every property which is preserved under transition to a continuous image is, like any property of Hausdorff spaces inherited by closed subspaces, stable under passage to a retract. As a result, compactness, connectedness, path-connectedness, separability, an upper bound on the dimension, paracompactness, normality, local compactness, and local connectedness are preserved under passage to a retract. At the same time, a retract of a space may have a simpler structure than the space itself, and be more amenable and convenient for specific research. Thus, a one-point set is a retract of an interval, of a straight line, of a plane, etc. If the space
. Every non-empty closed subset of the Cantor perfect set is a retract of it. In the transition from a space to a retract of it many important properties are preserved. In particular, every property which is preserved under transition to a continuous image is, like any property of Hausdorff spaces inherited by closed subspaces, stable under passage to a retract. As a result, compactness, connectedness, path-connectedness, separability, an upper bound on the dimension, paracompactness, normality, local compactness, and local connectedness are preserved under passage to a retract. At the same time, a retract of a space may have a simpler structure than the space itself, and be more amenable and convenient for specific research. Thus, a one-point set is a retract of an interval, of a straight line, of a plane, etc. If the space  has the fixed point property, i.e. if for each continuous transformation
has the fixed point property, i.e. if for each continuous transformation  there is a point
there is a point 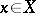 such that
such that 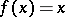 , then each retract of
, then each retract of 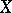 possesses the fixed point property too. In particular, the
possesses the fixed point property too. In particular, the  -dimensional sphere is not a retract of the
-dimensional sphere is not a retract of the 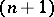 -dimensional ball of a Euclidean space, where
-dimensional ball of a Euclidean space, where 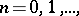 since the closed ball has the fixed point property (Brouwer's fixed-point theorem), and the sphere does not. A subspace
since the closed ball has the fixed point property (Brouwer's fixed-point theorem), and the sphere does not. A subspace 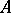 of a space
of a space  is called a neighbourhood retract of this space if there is in
is called a neighbourhood retract of this space if there is in 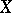 an open subspace which contains
an open subspace which contains 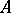 and of which
and of which  is a retract. The concept of a retract is directly related to the problem of the extension of continuous mappings. Thus, a subspace
is a retract. The concept of a retract is directly related to the problem of the extension of continuous mappings. Thus, a subspace 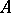 is a retract of
is a retract of 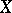 if and only if every continuous mapping of
if and only if every continuous mapping of 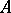 into an arbitrary topological space
into an arbitrary topological space  can be extended to a continuous mapping of the entire space
can be extended to a continuous mapping of the entire space 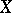 into
into  .
.
A metric space  is called an absolute retract (absolute neighbourhood retract) if it is a retract (neighbourhood retract) of every metric space containing
is called an absolute retract (absolute neighbourhood retract) if it is a retract (neighbourhood retract) of every metric space containing  as a closed subspace. For a metric space
as a closed subspace. For a metric space  to be an absolute retract it is necessary that it be a retract of some convex subspace of a normed linear space, and it is sufficient that
to be an absolute retract it is necessary that it be a retract of some convex subspace of a normed linear space, and it is sufficient that 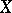 be a retract of a convex subspace of a locally convex linear space.
be a retract of a convex subspace of a locally convex linear space.
Thus, all convex subspaces of locally convex linear spaces are absolute retracts; such is the case, in particular, with a point, an interval, a ball, a straight line, etc. This characterization means that absolute retracts have the following properties. Every retract of an absolute retract is again an absolute retract. Each absolute retract is contractible in itself and is locally contractible. All homology, cohomology, homotopy, and cohomotopy groups of an absolute retract are trivial. A metric space  is an absolute retract if and only if, given any metric space
is an absolute retract if and only if, given any metric space  , a closed subspace
, a closed subspace 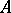 of
of  and a continuous mapping of
and a continuous mapping of 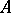 into
into 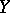 , the mapping can be extended to a continuous mapping of the entire space
, the mapping can be extended to a continuous mapping of the entire space  into
into 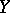 . Absolute neighbourhood retracts are characterized as retracts of open subsets of convex subspaces of normed linear spaces. They include all compact polyhedra. An important property of them is their local contractibility.
. Absolute neighbourhood retracts are characterized as retracts of open subsets of convex subspaces of normed linear spaces. They include all compact polyhedra. An important property of them is their local contractibility.
If a retraction of a space 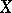 into a subspace
into a subspace 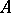 of
of 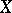 is homotopic to the identity mapping of
is homotopic to the identity mapping of 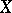 into itself, then
into itself, then 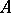 is called a deformation retract of
is called a deformation retract of  . A deformation retract of a space
. A deformation retract of a space 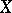 is homotopy equivalent to
is homotopy equivalent to 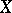 , i.e. they have the same homotopy type. Conversely, two homotopy-equivalent spaces can always be imbedded in a third space in such a way that they are both deformation retracts of this space.
, i.e. they have the same homotopy type. Conversely, two homotopy-equivalent spaces can always be imbedded in a third space in such a way that they are both deformation retracts of this space.
References
| [1] | K. Borsuk, "Theory of retracts" , PWN (1967) |
Comments
"Absolute retract" and "absolute neighbourhood retract" are often abbreviated to AR and ANR.
Retracts and absolute retracts have been studied in other classes of spaces than the metrizable ones, most successfully in compact Hausdorff spaces and in 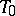 -spaces. A compact Hausdorff absolute retract is the same thing as a retract of a Tikhonov cube. If such a space is finite-dimensional (in the sense of covering dimension), it is metrizable, [a1]. The
-spaces. A compact Hausdorff absolute retract is the same thing as a retract of a Tikhonov cube. If such a space is finite-dimensional (in the sense of covering dimension), it is metrizable, [a1]. The  -absolute retracts or injective
-absolute retracts or injective 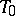 -spaces have a natural partial ordering which makes them continuous lattices (cf. Continuous lattice).
-spaces have a natural partial ordering which makes them continuous lattices (cf. Continuous lattice).
References
| [a1] | E.S. Shchepin, "A finite-dimensional compact absolute neighborhood retract is metrizable" Soviet Math. Doklady , 18 (1977) pp. 402–406 Dokl. Akad. Nauk SSSR , 233 : 3 (1977) pp. 304–307 |
| [a2] | J. van Mill, "Infinite-dimensional topology, prerequisites and introduction" , North-Holland (1988) |
Retract of a topological space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Retract_of_a_topological_space&oldid=17827