Residue of an analytic function
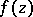 of one complex variable at a finite isolated singular point
of one complex variable at a finite isolated singular point  of unique character
of unique character
The coefficient  of
of 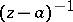 in the Laurent expansion of the function
in the Laurent expansion of the function 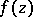 (cf. Laurent series) in a neighbourhood of
(cf. Laurent series) in a neighbourhood of  , or the integral
, or the integral
 |
where 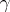 is a circle of sufficiently small radius with centre at
is a circle of sufficiently small radius with centre at  , which is equal to it. The residue is denoted by
, which is equal to it. The residue is denoted by 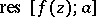 .
.
The theory of residues is based on the Cauchy integral theorem. The residue theorem is fundamental in this theory. Let 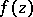 be a single-valued analytic function everywhere in a simply-connected domain
be a single-valued analytic function everywhere in a simply-connected domain 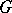 , except for isolated singular points; then the integral of
, except for isolated singular points; then the integral of 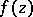 over any simple closed rectifiable curve
over any simple closed rectifiable curve 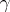 lying in
lying in  and not passing through the singular points of
and not passing through the singular points of 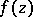 can be computed by the formula
can be computed by the formula
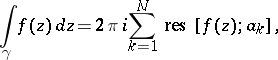 |
where 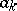 ,
, 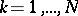 , are the singular points of
, are the singular points of 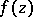 inside
inside 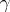 .
.
The residue of a function at the point at infinity 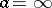 , for a function
, for a function 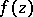 which is single-valued and analytic in a neighbourhood of that point, is defined by the formula
which is single-valued and analytic in a neighbourhood of that point, is defined by the formula
 |
where 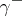 is a circle of sufficiently large radius, oriented clockwise, while
is a circle of sufficiently large radius, oriented clockwise, while  is the coefficient of
is the coefficient of 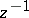 in the Laurent expansion of
in the Laurent expansion of 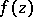 in a neighbourhood of the point at infinity. The residue theorem implies the theorem on the total sum of residues: If
in a neighbourhood of the point at infinity. The residue theorem implies the theorem on the total sum of residues: If 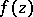 is a single-valued analytic function in the extended complex plane, except for a finite number of singular points, then the sum of all residues of
is a single-valued analytic function in the extended complex plane, except for a finite number of singular points, then the sum of all residues of 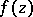 , including the residue at the point at infinity, is zero.
, including the residue at the point at infinity, is zero.
Thus, the computation of integrals of analytic functions along closed curves (contour integrals) is reduced to the computation of residues, which is particularly simple in the case of finite poles. Let 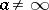 be a pole of order
be a pole of order 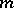 of the function
of the function 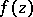 (cf. Pole (of a function)); then
(cf. Pole (of a function)); then
 |
If  (a simple pole), the formula becomes
(a simple pole), the formula becomes
 |
if 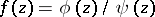 , where
, where  and
and 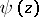 are regular in a neighbourhood of
are regular in a neighbourhood of  , and if
, and if  is a simple zero for
is a simple zero for 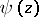 , then
, then
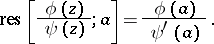 |
The application of the residue theorem to the logarithmic derivative yields the important theorem on logarithmic residues: If a function 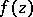 is meromorphic in a simply-connected domain
is meromorphic in a simply-connected domain  , while the simple closed curve
, while the simple closed curve 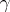 lies in
lies in  and does not pass through zeros or poles of
and does not pass through zeros or poles of 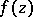 , then
, then
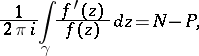 |
where 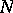 is the number of zeros and
is the number of zeros and  is the number of poles of
is the number of poles of 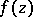 inside
inside 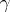 counted with multiplicities. The expression on the left-hand side of the formula is called the logarithmic residue of the function with respect to the curve
counted with multiplicities. The expression on the left-hand side of the formula is called the logarithmic residue of the function with respect to the curve 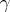 (see also Argument, principle of the).
(see also Argument, principle of the).
Residues are employed in computing certain integrals of real-valued functions, such as
 |
 |
where  is a rational function of
is a rational function of 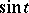 ,
, 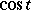 which is continuous if
which is continuous if 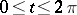 , and
, and 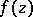 is a continuous function if
is a continuous function if  , where
, where 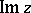 is the imaginary part of
is the imaginary part of  , and is analytic if
, and is analytic if  except for a finite number of singular points. By substituting
except for a finite number of singular points. By substituting 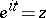 ,
, 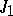 is reduced to the contour integral
is reduced to the contour integral
 |
i.e. to the computation of the residues;
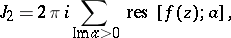 |
if 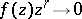 as
as 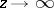 ,
, 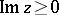 ,
, 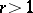 ; and
; and
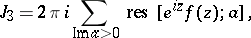 |
if 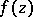 satisfies the conditions of the Jordan lemma.
satisfies the conditions of the Jordan lemma.
Residues have found numerous important applications in problems of analytic continuation, decomposition of meromorphic functions into partial fractions, summation of power series, asymptotic estimation, and many other problems of theoretical and applied analysis [1]–[4].
The theory of residues in one variable was mostly developed by A.L. Cauchy in 1825–1829. A number of results concerning the generalizations of the theory were obtained by Ch. Hermite (a theorem on the sum of the residues of doubly-periodic functions), P. Laurent, Yu.V. Sokhotskii, E. Lindelöf, and others.
Residues of analytic differentials rather than residues of analytic functions are studied on Riemann surfaces [5] (cf. also Differential on a Riemann surface). The residue of an analytic differential 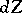 in a neighbourhood of (one of) its isolated singular points is defined as the coefficient
in a neighbourhood of (one of) its isolated singular points is defined as the coefficient  of
of 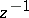 in the Laurent expansion of the function
in the Laurent expansion of the function 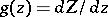 , where
, where  is a uniformizing parameter (cf. Uniformization) in a neighbourhood of this point. The integral of
is a uniformizing parameter (cf. Uniformization) in a neighbourhood of this point. The integral of  along any closed curve on the Riemann surface can be expressed in terms of the residues of the differential
along any closed curve on the Riemann surface can be expressed in terms of the residues of the differential  and its cyclic periods (the integrals of
and its cyclic periods (the integrals of  along canonical cuts, cf. Canonical sections). The theorem on the total sum of residues is applicable to Riemann surfaces: The sum of all residues of a meromorphic differential on a compact Riemann surface is zero.
along canonical cuts, cf. Canonical sections). The theorem on the total sum of residues is applicable to Riemann surfaces: The sum of all residues of a meromorphic differential on a compact Riemann surface is zero.
The theory of residues of analytic functions of several complex variables.
See [8]–[10], [12], [13]. This theory is based on the integral theorems of Stokes and Cauchy–Poincaré, which make it possible to replace the integral of a closed form along one cycle by an integral of this form along another cycle which is homologous to the former. The foundations of the theory of residues of functions of several variables were laid by H. Poincaré [6], who was the first (1887) to generalize Cauchy's integral theorem and the concept of a residue to functions of two complex variables; he showed, in particular, that the integral of a rational function of two complex variables along a two-dimensional cycle which does not pass through the singularities of the integrand can be reduced to the periods of Abelian integrals (cf. Abelian integral), and employed double residues as the basis of a two-dimensional analogue of Lagrange series.
J. Leray [7] (see also [4], [8]) developed the general theory of residues on a complex-analytic manifold  . Leray's residue theory describes, in particular, a method of computing integrals along certain cycles on
. Leray's residue theory describes, in particular, a method of computing integrals along certain cycles on 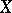 of closed exterior differential forms with singularities on analytic submanifolds. He introduced the concept of a residue form, which generalizes the concept of a residue of an analytic function of a single variable; the residue formula thus obtained makes it possible to reduce the computation of the integral of a form
of closed exterior differential forms with singularities on analytic submanifolds. He introduced the concept of a residue form, which generalizes the concept of a residue of an analytic function of a single variable; the residue formula thus obtained makes it possible to reduce the computation of the integral of a form 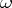 with a first-order polar singularity on a complex-analytic submanifold
with a first-order polar singularity on a complex-analytic submanifold 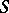 along a given cycle in
along a given cycle in  to the computation of an integral of the residue form
to the computation of an integral of the residue form  along a cycle on
along a cycle on 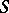 of one dimension lower. In calculating integrals of closed forms with arbitrary singularities on
of one dimension lower. In calculating integrals of closed forms with arbitrary singularities on 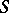 , the important concepts are those of a residue class (cf. Residue form) and the Leray theorem, according to which any closed form
, the important concepts are those of a residue class (cf. Residue form) and the Leray theorem, according to which any closed form 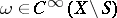 has a corresponding cohomologous form
has a corresponding cohomologous form 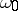 with a first-order polar singularity on
with a first-order polar singularity on 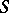 . For a form
. For a form 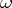 with a singularity on several submanifolds
with a singularity on several submanifolds 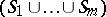 one uses the composite residue form
one uses the composite residue form
 |
the residue class
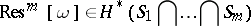 |
and the residue formula
 |
where 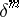 is the composite Leray coboundary operator associated to the Leray coboundary operator
is the composite Leray coboundary operator associated to the Leray coboundary operator 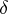 and
and 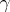 is a cycle in
is a cycle in 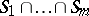 .
.
There exists another approach to the theory of residues of functions of several complex variables — the method of distinguishing a homology basis, based on an idea of E. Martinelli and involving the use of Alexander duality [8]. Let 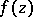 ,
, 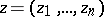 , be a holomorphic function in a domain
, be a holomorphic function in a domain 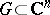 , and let
, and let 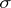 be an
be an  -dimensional cycle in
-dimensional cycle in 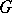 . If
. If 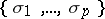 is a basis of the
is a basis of the  -dimensional homology space of the domain
-dimensional homology space of the domain 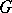 and
and
 |
is the expansion of 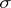 with respect to this basis, a generalization of the residue theorem has the form
with respect to this basis, a generalization of the residue theorem has the form
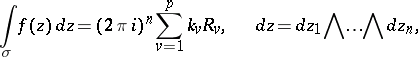 |
where
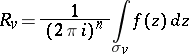 |
is an  -dimensional analogue of the residue and is called the residue of the function
-dimensional analogue of the residue and is called the residue of the function 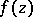 with respect to the basic cycle
with respect to the basic cycle  . As distinct from the case of one variable, it is very difficult to find both a homology basis
. As distinct from the case of one variable, it is very difficult to find both a homology basis 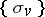 and the coefficients
and the coefficients 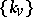 . In several cases (for example, when
. In several cases (for example, when  , where
, where 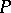 is a polynomial) these problems may be solved with the aid of Alexander–Pontryagin duality. The coefficients
is a polynomial) these problems may be solved with the aid of Alexander–Pontryagin duality. The coefficients 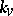 are found as the linking coefficients of the cycle
are found as the linking coefficients of the cycle 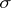 with the cycles on the set
with the cycles on the set 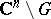 (compactified in a certain manner) which are dual to the cycles
(compactified in a certain manner) which are dual to the cycles 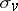 . The residues
. The residues 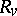 can in some cases be found as the respective coefficients of the Laurent expansion of the function
can in some cases be found as the respective coefficients of the Laurent expansion of the function 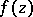 .
.
Multi-dimensional analogues of logarithmic residues [4], [8]–[9] express the number of common zeros (counted with multiplicities) of a system of holomorphic functions  in a domain
in a domain 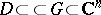 by means of the integrals
by means of the integrals
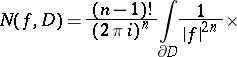 |
 |
 |
where 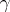 is some cycle in
is some cycle in 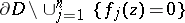 . Residues of functions of several variables have found use in the study of Feynman integrals, in combinatorial analysis [11] and in the theory of implicit functions [8].
. Residues of functions of several variables have found use in the study of Feynman integrals, in combinatorial analysis [11] and in the theory of implicit functions [8].
References
| [1] | A.I. Markushevich, "Theory of functions of a complex variable" , 1 , Chelsea (1977) (Translated from Russian) |
| [2] | M.A. Evgrafov, "Analytic functions" , Saunders , Philadelphia (1966) (Translated from Russian) |
| [3] | I.I. [I.I. Privalov] Priwalow, "Einführung in die Funktionentheorie" , 1–3 , Teubner (1958–1959) (Translated from Russian) |
| [4] | B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1985) (In Russian) |
| [5] | G. Springer, "Introduction to Riemann surfaces" , Addison-Wesley (1957) pp. Chapt.10 |
| [6] | H. Poincaré, "Sur les résidues des intégrales doubles" Acta Math. , 9 (1887) pp. 321–380 |
| [7] | J. Leray, "Le calcule différentiel et intégral sur une variété analytique complexe (Problème de Cauchy, III)" Bull. Soc. Math. France , 87 (1959) pp. 81–180 |
| [8] | L.A. Aizenberg, A.P. Yuzhakov, "Integral representations and residues in multidimensional complex analysis" , Transl. Math. Monogr. , 58 , Amer. Math. Soc. (1983) (Translated from Russian) |
| [9] | A.K. Tsikh, "Multidimensional residues and its applications" , Amer. Math. Soc. (Forthcoming) (Translated from Russian) |
| [10] | P.A. Griffiths, "On the periods of certain rational integrals I" Ann. of Math. (2) , 90 : 3 (1969) pp. 460–495 |
| [11] | G.P. Egorichev, "Integral representation and the computation of combinatorial sums" , Amer. Math. Soc. (1984) (Translated from Russian) |
| [12] | P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , Wiley (Interscience) (1978) |
| [13] | W.R. Coleff, M.F. Herrera, "Les courants residuals associés à une forme meromorphe" , Lect. notes in math. , 633 , Springer (1978) |
Comments
See also the comments and references to Residue form.
References
| [a1] | D.S. Mitrinović, J.D. Kečkić, "The Cauchy method of residues: theory and applications" , Reidel (1984) |
Residue of an analytic function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Residue_of_an_analytic_function&oldid=17749